Medium 好讀版點此。

在 Day 3 的文章尾聲，我們發現：就算檔名不同，只要內容相同，就會產出一樣的雜湊碼，例如：

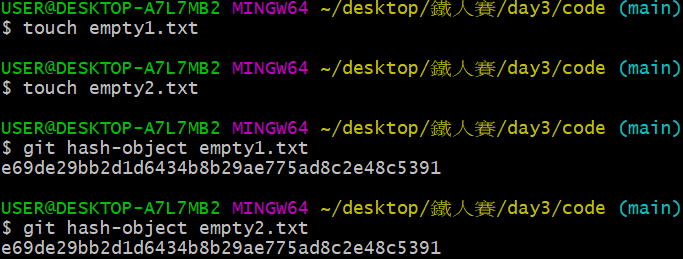
empty1.txt 跟 empty2.txt 都是空文字檔，產出的雜湊碼都是 e69de29...，由此我們可以發現，這雜湊碼並非隨機產生的亂碼，而是經歷一套規則產生。

安全雜湊演算法

英文全名為 Secure Hash Algorithm，簡稱 SHA，是由美國國家標準技術研究所（National Institute of Standards and Technology，簡稱 NIST）頒布的標準，這些雜湊函式共有下列五大目標：

1. 輸入相同，則輸出也要相同：如上述範例所示，只要輸入內容一樣，跑出來的雜湊碼也要一樣，不能同樣內容進去，卻跑出不同結果。
2. 輸出長度永遠相同：不論輸入是沒有任何內容、少少的位元資料或一筆龐大資料，最終產生的雜湊碼必為 40 位數。
3. 雪崩效應（avalanche effect）：哪怕輸入只發生了微小的改變，輸出結果也要大大不同。
4. 無法逆向破解：不能像線性函數 y = ax + b 這樣能用 x = (y-b)/a 去反推輸入，才能確保安全性。
5. 均勻分布、避免碰撞：若輸入相異、輸出卻相同稱為「雜湊碰撞（hash collision）」，演算法應避免這樣的碰撞產生。

要同時達成上述四條件感覺好玄，這演算法到底是有什麼神奇魔力，可以達成以上五大目標？讓我們以 git 最開始使用的 SHA-1 雜湊（SHA 的其中一種版本）流程，來看看這加密雜湊函式到底在變什麼魔法。

SHA-1 演算法流程

以上述空白檔案為例，在進入 SHA-1 演算法本體前，會變成：

<object type> <size><\0><content>

這裡建立的 <object type> 是 blob、<size> 為 0、<content> 為空，因此代換後變成：

blob 0\0

這個 blob 0\0 便是 SHA-1 函數的輸入。

值得留意的是，當中包含的資訊僅有「內容」與「內容長度」，而沒有檔案名稱等元資料，因此，文章最開始範例的 empty1.txt 與 empty2.txt 雖然檔名不同，但因為內容一樣（皆為空檔案）、內容長度也一樣（皆為 0），兩者又都是要建立 blob 物件，因此，送進去 SHA-1 函數的輸入自然也一樣，

進入 SHA-1 演算法核心

在取得 blob 0\0 這輸入後，要先對照 ASCII 表轉換成十進制數字（\0為終止符號，因此 ASCII 碼為 0）：

98 108 111 98 32 48 0

接著再將十六進制數字轉為二進制：

1100010 1101100 1101111 1100010 100000 110000 0

每個數字應有八位元，若不足八位元，則補上前導 0：

01100010 01101100 01101111 01100010 00100000 00110000 00000000

然後再把這些數字串起來：

01100010011011000110111101100010001000000011000000000000

接下來的步驟沒辦法在有限篇幅中以實例呈現，讓我們改以圖示說明觀念。

目前我們在圖示左上角的紅色星星處，後續步驟號碼可對照下方文字說明：

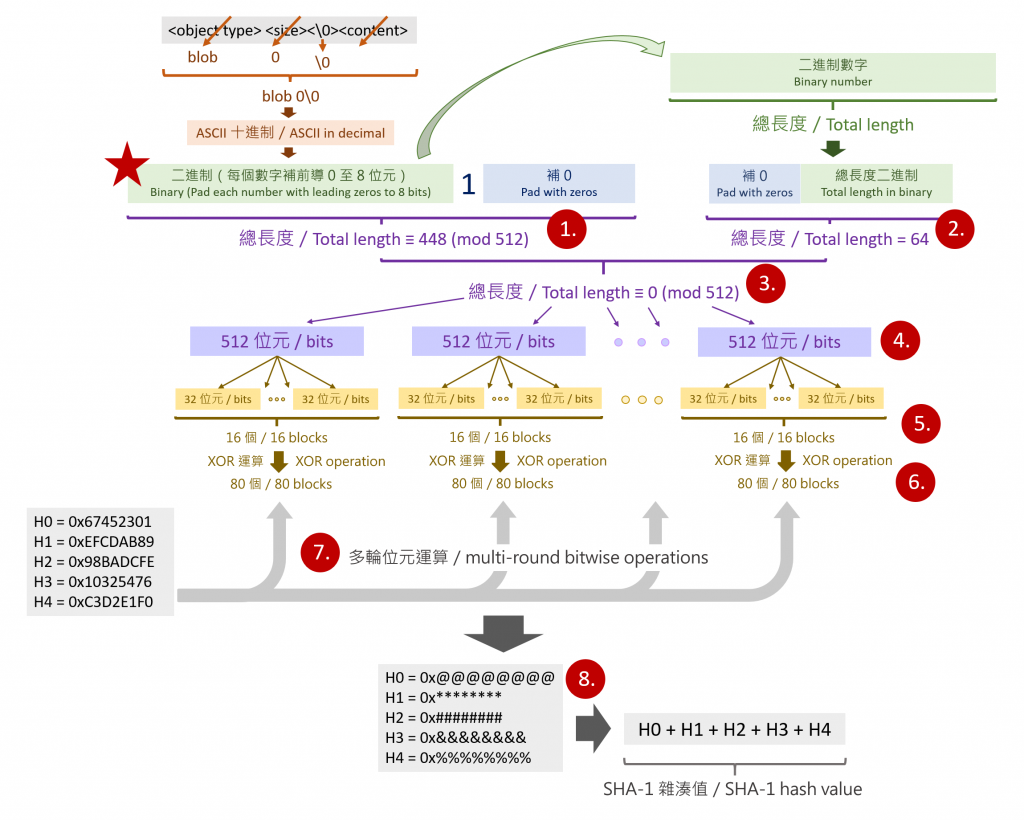
SHA-1 演算法流程圖解

1. 在二進制數字最後補 1 表示終結，後面再補 0 至總長度以 512 模除會得 448 為止（也就是除以 512 後的餘數是 448，這樣再加上 64 就可以被 512 整除）。
2. 把剛剛的二進制數字的「總長度」這個值轉為二進制，再將總長度值二進制的數字往前補 0 至總長度為 64 位元。
3. 第 1. 步得到的長度差 64 位元可被 512 整除、第 2. 步得到的長度就是 64 位元，兩者組合成一個總長度為 512 倍數的二進制數字。
4. 把 3. 組合出的二進制數字，以 512 位元為單位，拆成多個小塊。
5. 把 4. 拆出來的 512 位元小塊，再個拆成 16 個長度為 32 位元的小塊。
6. 第 5. 步拆出的 32 位元小塊經多次 XOR 位元運算後，小塊數量從 16 個變 80 個。
7. 取 H0 H1 H2 H3 H4 五個十六進制的數字，與 6. 產生的 80 個小塊做多輪超級複雜的位元運算，產生新的 H0 H1 H2 H3 H4 。
8. 把新 H0 H1 H2 H3 H4 串在一起，就是最終的雜湊碼。

這些步驟已經讓人看得頭昏眼花，但其實以上說明還忽略了非常多細節，其中又以第 7. 步最為複雜。若對當中的詳細流程有興趣，可參考 ajalt/python-sha1 這個 GitHub 倉儲，以 Python 程式碼實現 SHA-1 的運算過程。

或者我們可以單純做個實驗觀察，透過 git clone 取得該倉儲後，以終端機指令 printf 提供 blob 0\0 的格式化標準輸出給 sha1.py 當引數，即可得空 blob 物件會產生的雜湊碼 e69de29...：

SHA-1 如何達到雜湊演算法五大目標

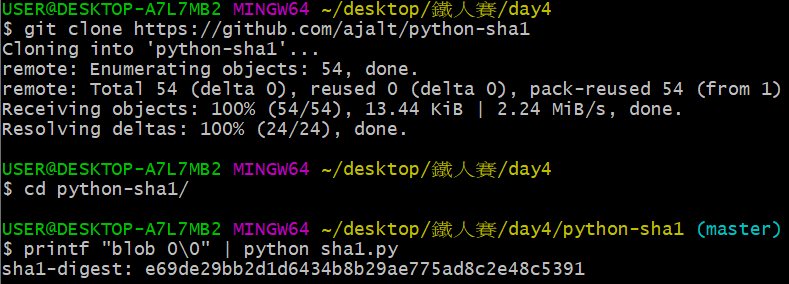
在對 SHA-1 流程有基本認識後，我們可以用直觀的方式，大致感受這演算法如何達成上述的五大目標（嚴謹的數學證明屬於密碼學範疇，大幅超越 git 文章所要探討的難度）：

1. 輸入相同，則輸出也要相同：所有輸入都是經過「固定步驟」走到最後，只要輸入內容一樣，也都經過一樣的運算流程，則輸出結果必相同。
2. 輸出長度永遠相同：最終輸出仰賴在第 7. 步對 H0 H1 H2 H3 H4 的大量複雜運算，但不管怎麼算，這五個數都是 8 位數，等到第 8. 步串在一起，則必為 40 位數。
3. 雪崩效應：輸入拆成多個小塊後會加大運算量，且過程中有多個步驟依賴前面的運算結果，導致輸入的些微差距被放大再放大。
4. 無法逆向破解：許多小步驟依賴前面的運算結果，且過程中每次的模運算都會丟失一些資訊，讓逆向推導無法達成。
5. 均勻分布、避免碰撞：過程經過補 0、拆小塊、多重位元運算等步驟，在發明時被認為能有效避免碰撞發生。

值得留意的是，這五大目標的第 5. 點「均勻分布、避免碰撞」已隨著運算技術進步而被破解，因此 SHA-1 現在已被認為是不安全的雜湊演算法，連 git 都在其官方頁面中提及，要從 SHA-1 轉換到更安全的 SHA-256。

所以為什麼要用 SHA 碼當 Git 識別碼？

我們花了很多篇幅在講 SHA-1 是怎麼算的，但回到最根本的問題是：為什麼 git 要用雜湊碼當識別碼？難道用簡單一點的編號方式，產生每個 git 物件的識別碼不好嗎？還是有什麼資安考量？

來看看 git 官方文件怎麼說的

Git 在官方文件中提到使用雜湊碼具有以下兩優點：

1. 檢查完整性相對容易：因為雪崩效應，哪怕只是一個位元反轉，產生的變化會非常大，因此，若資料有異動，可以很容易察覺。
2. 尋找物件很快：在沒有雜湊衝突的情況下，一組代碼就代表唯一的物件，因此，要找到目標 git 物件非常快。

有了上述兩點特性，一組雜湊碼就能代表唯一且不可變的項目。

來聽聽 Git 發明人 Linus 怎麼說的

雖然上述 git 文件另有提及使用雜湊碼在資安上的額外好處，但在《Tech Talk: Linus Torvalds on git》這場演講中，git 的發明人 Linus Torvalds 則特別強調：使用雜湊碼不是用來處理資安議題，而是要確保資料的一致性。

這就呼應剛剛在文件裡得出的結論：一組雜湊碼就能代表唯一且不可變的項目，當多人協作或橫跨不同平臺時，我們都可以知道「這組雜湊碼對應的檔案內容就是長這樣」，哪怕數年後再把檔案放到其他地方儲存，只要雜湊碼不變，我們就能確定這份檔案（或者說 git 物件）裡面是連「一個位元都沒有被動過」。

小結

Git 使用密碼學中的 SHA 雜湊碼來當作物件的識別，並不是有特別的資安考量，而是可用來確保檔案的一致性。

參考資料

1. 【冷知識】那個長得很像亂碼 SHA-1 是怎麼算出來的？
2. 數論與密碼學 (Python, JavaScript)
3. ASCII 表
4. ajalt/python-sha1
5. Shell printf 命令
6. SHA-1 是什麼？為什麼不再安全？
7. Migrate Git from SHA-1 to a stronger hash function.
8. We have broken SHA-1 in practice.
9. Why does Git use a cryptographic hash function?
10. Tech Talk: Linus Torvalds on git