經過前五天的努力，我們已經成功打造出一個功能完整的互動式學習地圖平台了！

從第一天提出 GASO 的概念，到第二天決定使用 Graphviz 來繪製地圖，再到第三天建立 Google Sheets 作為資料後台，第四天調整出多種美觀的排版效果，最後第五天添加了節點點擊互動功能。

現在這個地圖已經可以點擊節點查看詳細資訊了，但還有一個重要的問題：

當使用者點擊一個節點時，如何清楚顯示到達該節點的學習路徑？

就像使用 GPS 導航時，系統會高亮顯示從起點到終點的路線一樣，我們的學習地圖也應該要能夠高亮顯示學習路徑，讓學習者清楚知道要達到目標需要經過哪些步驟。

所以今天，我們要讓學習路徑「亮」起來！就像這樣：

路徑高亮功能的核心價值

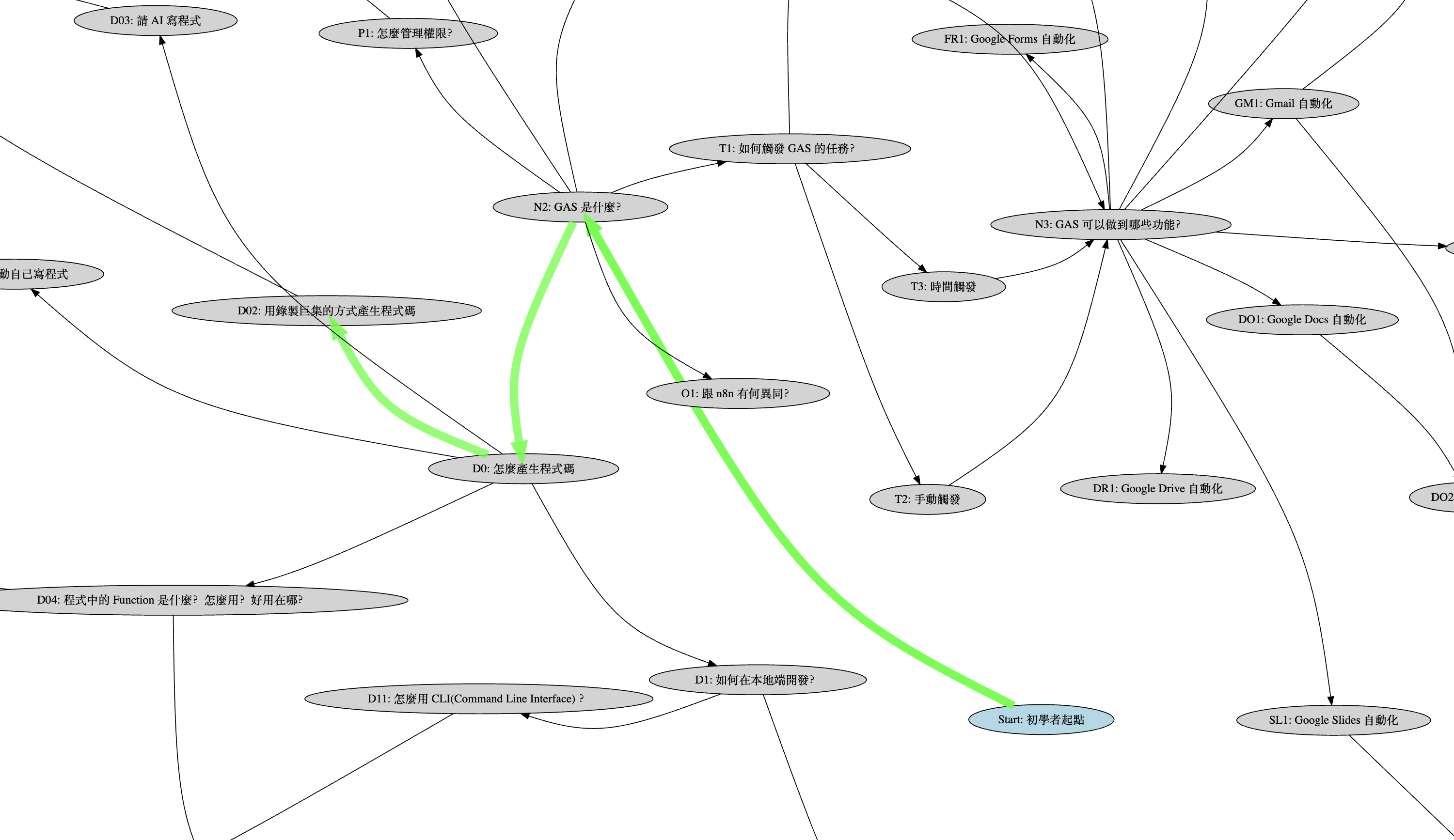
在我想像中的 GASO 平台，當使用者點擊任何一個節點時，系統應該要能夠：

1. 自動找到學習路徑：從學習起點到目標節點的所有可能路徑
2. 視覺化高亮顯示：用顏色和動畫效果突出顯示這些路徑
3. 多路徑支援：同一目標可能有多條學習路徑，都要能清楚顯示

這樣一來，學習者就能像看地圖一樣，一眼看出要達到目標需要經過哪些關卡，讓學習變得更有方向感。

技術實作：路徑查找演算法

圖論基礎：鄰接表建立

在開始實作之前,我們先來了解一下什麼是鄰接表(Adjacency List)。

鄰接表是一種用來表示圖(Graph)的資料結構,它用一個陣列或物件來儲存圖中所有的節點,每個節點再連結一個列表,記錄與該節點相鄰的所有節點。

舉個例子,假設我們有一個簡單的學習地圖:

• 節點 A 可以到達 B 和 C
• 節點 B 可以到達 D
• 節點 C 可以到達 D
• 節點 D 沒有出邊

用鄰接表表示就會是:

{
  A: [B, C],
  B: [D],
  C: [D],
  D: []
}

這樣我們就可以快速查詢任何節點可以到達哪些其他節點。比如要查詢節點 A 可以到達哪些節點，只需要查看 adjacencyList['A']，就能得到 [B, C]。

在我們的 GASO 專案中，鄰接表是這樣建立的：

// 建立鄰接表用於路徑查找
// 鄰接表是一種圖的資料結構，用來記錄每個節點與哪些節點相連
const adjacencyList = {};

// 初始化鄰接表
// 為每個節點建立一個空陣列，用來存放與它相連的節點
nodes.forEach(([id]) => {
  if (id) {
    adjacencyList[id] = []; // 每個節點對應一個空陣列
  }
});

// 建立鄰接關係
// 根據邊的資料，將相連的節點加入到彼此的鄰接表中
edges.forEach(([src, tgt]) => {
  if (src && tgt) {
    // 如果來源節點還沒有鄰接表，先建立一個
    if (!adjacencyList[src]) {
      adjacencyList[src] = [];
    }
    // 將目標節點加入到來源節點的鄰接表中
    adjacencyList[src].push(tgt);
  }
});

鄰接表是一個物件，其中每個鍵是節點 ID，值是一個陣列，包含該節點可以直接到達的所有節點。

起點識別：找到學習的起點

在學習地圖中，起點是那些沒有入邊(也就是沒有上游、只有下游)的節點，也就是學習者開始學習的地方。在我們的實作中，系統會自動找出所有沒有入邊的節點作為起點：

/**
 * 找出學習路徑圖中的起始節點
 * 起始節點是指沒有其他節點指向它的節點，即沒有入邊的節點
 * @returns {Array} 起始節點陣列
 */
function findStartNodes() {
  // 取得所有節點（從鄰接表的鍵值中取得）
  const allNodes = new Set(Object.keys(state.adjacencyList));
  
  // 用來記錄哪些節點有入邊（被其他節點指向）
  const hasIncoming = new Set();
  
  // 遍歷鄰接表，找出所有有入邊的節點
  Object.entries(state.adjacencyList).forEach(([source, neighbors]) => {
    // 對於每個源節點，檢查它指向的所有鄰居節點
    neighbors.forEach(neighbor => {
      // 將被指向的節點標記為有入邊
      hasIncoming.add(neighbor);
    });
  });
  
  // 起始節點是沒有入邊的節點（即沒有被其他節點指向的節點）
  const startNodes = Array.from(allNodes).filter(node => !hasIncoming.has(node));
  
  return startNodes;
}

路徑查找：BFS演算法應用

我們使用廣度優先搜尋(BFS)來找到從起點到目標節點的所有可能路徑：

為什麼選擇BFS？

在學習路徑規劃中，選擇BFS有以下幾個重要原因：

1. 保證最短路徑優先：BFS會先探索距離起點較近的節點，這意味著我們會優先找到最短的學習路徑。對於學習者來說，最短的路徑通常代表最直接的學習順序。

2. 避免無限循環：在圖形結構中，如果存在循環路徑，BFS的層級探索特性可以幫助我們避免在同一個節點上無限循環，確保演算法的終止性。

3. 找到所有可能路徑：與深度優先搜尋(DFS)不同，BFS可以系統性地探索所有可能的路徑，不會遺漏任何一條從起點到終點的路徑。

4. 記憶體使用可控：雖然BFS需要儲存所有待探索的路徑，但在學習地圖的規模下，這個記憶體開銷是可接受的，而且比DFS的遞迴調用堆疊更可預測。

5. 適合學習路徑的特性：學習路徑通常具有層級結構（基礎→進階），BFS的層級探索方式正好符合這種結構特性。

function findAllPaths(start, target) {
  const allPaths = [];
  const queue = [[start]]; // 佇列中儲存路徑
  
  while (queue.length > 0) {
    const path = queue.shift();
    const current = path[path.length - 1];
    
    if (current === target) {
      // 找到目標節點，記錄這條路徑
      allPaths.push([...path]);
      continue;
    }
    
    const neighbors = state.adjacencyList[current] || [];
    
    for (const neighbor of neighbors) {
      // 避免循環路徑（同一個節點在路徑中出現多次）
      if (!path.includes(neighbor)) {
        const newPath = [...path, neighbor];
        queue.push(newPath);
      }
    }
  }
  
  return allPaths;
}

這個演算法會找到所有從起點到目標節點的路徑，並且避免循環路徑。

整合路徑查找功能

現在我們需要將這些功能整合到現有的系統中：

/**
 * 找到到達指定節點的所有路徑
 * @param {string} targetNodeId - 目標節點ID
 * @returns {Array} 所有可能的路徑陣列
 */
function findPathToNode(targetNodeId) {
  const startNodes = findStartNodes();
  const allPaths = [];
  
  // 從每個起點開始尋找路徑
  startNodes.forEach(startNode => {
    const paths = findAllPaths(startNode, targetNodeId);
    allPaths.push(...paths);
  });
  
  return allPaths;
}

今天的成果

透過今天的實作，我們成功建立了完整的路徑查找系統：

1. 鄰接表建立：將學習地圖轉換為可操作的圖形資料結構
2. 起點識別：自動找出學習的起始節點
3. 路徑查找：使用BFS演算法找到所有可能的學習路徑
4. 循環避免：確保路徑查找不會陷入無限循環

明天我們將繼續實作視覺化高亮功能，讓這些找到的路徑能夠以美觀的方式呈現在使用者面前。

我們明天見！

如果想要看一些我的鐵人賽花邊心得，
也歡迎追蹤我的 Threads 和 Facebook