昨天介紹 Vector Space Model（向量空間模型）時，有講到 Cosine Similarity（餘弦相似度），但只是輕輕帶過💨，今天就來深入了解 Cosine Similarity 到底是拿來看什麼的？

講到 Cosine ，相信大家都已經回想起高中數學課學的 sinθ、cosθ、tanθ......

沒錯，這裡的 Cosine 就是數學上的概念。

Cosine Similarity是什麼

• Cosine Similarity 就是從計算兩個向量夾角的餘弦值，來衡量兩個向量的方向有多接近
• 昨天有講到這邊講的向量就是文本，文本可以利用 Word Embeddings、Bag-of-Words (BoW)等方式來轉換成向量
• Cosine Similarity 被廣泛運用在機器學習、資料分析、搜尋引擎
• 這個測量方式可以不用顧慮文本的長度不一
• 公式長這樣：

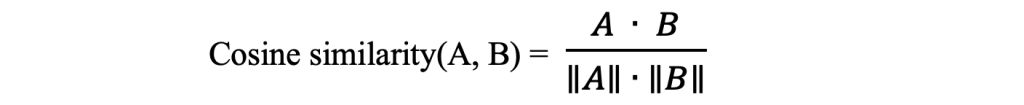
• A ∙ B ：向量 A 跟 B 的內積（dot product)

• ||A|| ∙ ||B|| = 向量 A 與 B 的普通乘積（regular product）
  （ ||A|| 和 ||B|| = 向量 A 與 B 的長度（大小） ）

• 數值會介於 -1 到 1：

  • 越接近 1 → 方向越相似

  • 越接近 0 → 幾乎不相關

  • 越接近 -1 → 方向相反

簡單來說，Cosine Similarity 告訴我們「兩個向量的方向有多相近」。

可以應用在哪？

• 資訊檢索：像 Google 搜尋，找到跟你輸入文字最相似的文件
• 推薦演算法：推薦相似的貼文、影片或是音樂

小總結

Cosine Similarity 其實蠻直觀的：

• 它看的是向量方向，越接近 → 越相似

• 它不會去看文本的長度 → 可以避免文章長短影響相似度

💡 它是向量空間模型裡的一個重要概念，也是許多自然語言處理（NLP）與機器學習應用的基礎，我們可以把它跟 TF-IDF、Word Embedding 等向量相關的技術結合！