在我們進入 SSH 和 https 等相關主題之前，我們先來稍微認識些簡單的密碼學。

密碼學基礎

編碼

• 跟密碼學無關
• 編碼（encoding）：將資訊從一種形式轉換成另一種形式的過程
• 解碼（decoding）：將編碼後的資訊轉換成編碼前的形式的過程
• EX: Base64、Morse code

補充：Base64

• 基於64個可顯示的字元（A~Z, a~z, 0~9）來表示一個二進位的資料
• 已知 2^6 = 64，所以每 6 個位元一組，一組用 1 個base64編碼表示
• 3 個位元組為24位元，用 4 個base64編碼表示
• 如果為空字元，則用= 代替（base64編碼最後不一定會有=！！！）
  字元轉base64示意圖
  

密碼學

• 跟密碼（password）沒關係
• 跟編碼（encoding）沒關係
• 跟隱寫術（Steganography）很不一樣
• 克勞德·夏農(Claude Elwood Shannon, 1916~2001)
  • 1948年，發布 通訊的數學原理(C. E. Shannon, 1948, A mathmatical theory of communication)，提出信息熵(Entropy) 去度量、壓縮、編碼信息(information)
  • 1949年，在信息熵的基礎上發表 保密系統的通信理論(C. E. Shannon, 1949, Communication Theory of Secrecy System)奠定密碼學基礎
• 在大量的數學原理中發現了少量的資安

那明文和數字有甚麼關係
=> 形式不同罷了
可以用 python 實作看看，具體如下

密碼學相關名詞解釋

• 明文（plain text）：加密前的訊息，解密後的訊息
• 密文（cipher text）：加密後的訊息，解密前的訊息
• 密碼學演算法：密碼學相關的程序（ex: 加密、解密etc...）的演算法
• 加密（Encrypt）：將明文透過某種程序轉換成密文
• 解密（Decrypt）：將密文透過某種程序轉換成明文
• 金鑰/ 密鑰（Key）: 加解密使用的鑰匙
• 密鑰空間：所有可能密鑰組成的集合稱為密鑰空間
• 信道 : 隔開通訊雙方的障礙，通常可以是網路或是物理上的距離

柯克霍夫原則（Kerckhoffs's Principle）

• 縱使這套系統的方方面面已經讓其他人知道了，但只要不知道其密鑰（key），那這套系統應該是安全可靠的
• 換句話說：真正強壯的加解密系統經過千錘百鍊後，應仍然能夠繼續確保其安全性

對稱式加密

• 又稱秘密金鑰密碼系統、單金鑰密碼系統
• 發送方和接收方會用共同的密鑰去做加解密，具體如下
  

非對稱式加密

• 1976年前開發的加密系統基本上都是對稱式加密
• 1976年, Whitfield Diffie 和 Martin Hellman發表 密碼學的新方向(New Direction in cryptography) 奠定公開金鑰密碼系統的基礎
• 發送方會用接收方的公鑰做加密，而接收方會用自己的私鑰做解密，具體如下
  

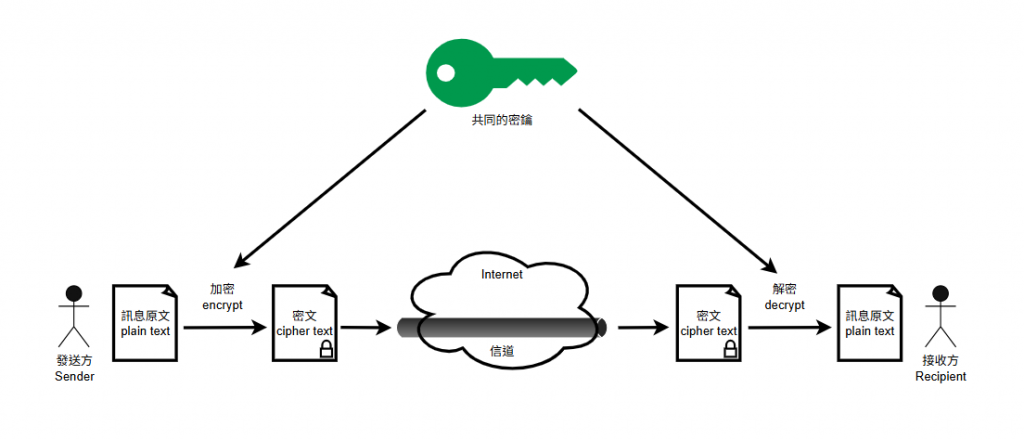
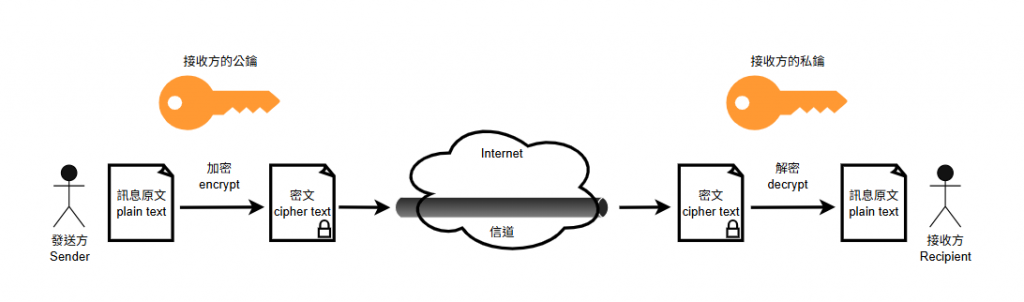
實際的應用我們下回再說