232. Implement Queue using Stacks

題目：
請你用 兩個 stack 來實作一個 先進先出 (FIFO) 的 queue，並實作以下方法：

• push(x)：將元素 x 推入 queue 尾端
• pop()：移除並回傳 queue 頭端的元素
• peek()：回傳 queue 頭端的元素
• empty()：判斷 queue 是否為空

範例：

• Example 1:
  Input
  ["MyQueue", "push", "push", "peek", "pop", "empty"]
  [[], [1], [2], [], [], []]
  Output
  [null, null, null, 1, 1, false]

Explanation
MyQueue myQueue = new MyQueue();
myQueue.push(1); // queue is: [1]
myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue)
myQueue.peek(); // return 1
myQueue.pop(); // return 1, queue is [2]
myQueue.empty(); // return false

—

想法：
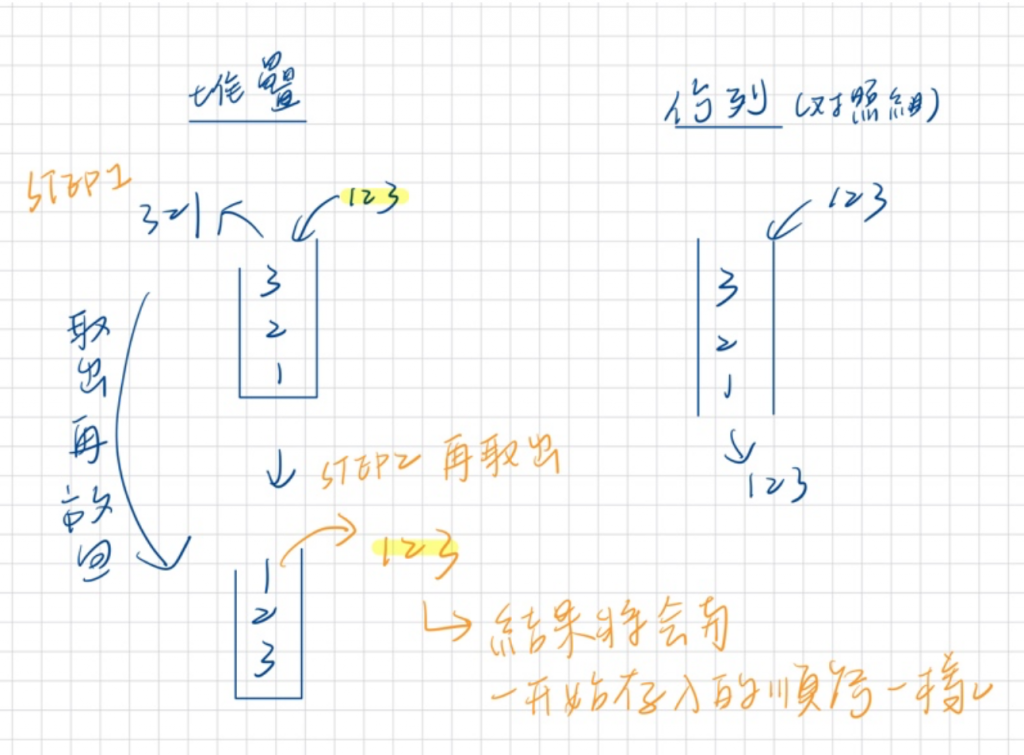
因為堆疊為先進後出，佇列為先進先出，因此為了能用堆疊實現佇列，所以需要創立兩個 stack 一個用於存放數據，另一個用來轉移。

—

程式碼：

class MyQueue {
    private Stack<Integer> stack1;
    private Stack<Integer> stack2;

    public MyQueue() {
        //建立兩個Stack
        stack1 = new Stack<>();
        stack2 = new Stack<>();
    }
    
    public void push(int x) {
        stack1.push(x); //將資料推入Stack1
    }
    
    public int pop() {
        //當Stack2是空，即可將Stack1資料放入
        if(stack2.isEmpty()){
            while (!stack1.isEmpty()){
                stack2.push(stack1.pop()); //將Stack1資料「取出」並「放回」Stack2
            }
        }
        return stack2.pop(); //再取出Stack2的資料——＞可達成用堆疊實現佇列
    }
    
    public int peek() {
        if (stack2.isEmpty()){
            while (!stack1.isEmpty()){
                stack2.push(stack1.pop()); 
            }
        }
        return stack2.peek(); //查看頭端資料
    }
    
    public boolean empty() {
        return stack1.isEmpty()&& stack2.isEmpty();
    }
}

—

實際操作：

stack1 = []
stack2 = []

STEP1:
push(1)
將 1 推入 stack1
stack1 = [1]
stack2 = []

STEP2:
push(2)
將 2 推入 stack1
stack1 = [1, 2] (左底右頂)
stack2 = []

STEP3:
peek()
stack2 為空 → 將 stack1 元素倒入 stack2
取出 stack1 頂 2 → push 到 stack2 → stack2 = [2]
取出 stack1 頂 1 → push 到 stack2 → stack2 = [2, 1]

stack1 = []
stack2 = [2, 1]

peek() → 查看 stack2 頂 → 回傳 1

STEP4:
pop()
stack2 非空 → 直接 pop stack2 頂元素 → 回傳 1

stack1 = []
stack2 = [2]

STEP5:
empty()
stack1 = []
stack2 = [2]
→ 不是空 → 回傳 false

STEP6:
push(3)
push 總是放入 stack1 → push(3)

stack1 = [3]
stack2 = [2]

STEP7:
pop()
stack2 非空 → 直接 pop stack2 頂元素 → 回傳 2

stack1 = [3]
stack2 = []

STEP8:
pop()
stack2 為空 → 需轉移
取出 stack1 頂 3 → push 到 stack2 → stack2 = [3]

stack1 = []
stack2 = [3]

pop() → 取出 stack2 頂元素 → 回傳 3

STEP9:
empty()
makefile
複製程式碼
stack1 = []
stack2 = []
——＞兩者皆空 ——＞回傳 true

最終：
peek() → 1
pop() → 1
empty()→ false
pop() → 2
pop() → 3
empty()→ true