17. Letter Combinations of a Phone Number

這道題目（電話號碼的字母組合)要求根據輸入的數字字串（只包含2到9的數字），找出所有可能的字母組合。
這是一道組合問題，每個數字對應一組字母，需要從每個數字對應的字母組中各選一個字母，將它們組合成一個新的字串。例如，數字2對應{a, b, c}，數字3對應{d, e ,f}，那麼組合就會是a配d, e, f；b配d, e, f；c配d, e, f，總共有3 x 3 = 9種組合。

要解決這類所有組合（或排列）的問題，回溯法（Backtracking）是最常見且高效的演算法模式。
首先，先介紹下回溯法，回溯法可以想像成是深度優先搜尋(DFS)在遍歷決策樹上的應用，分成決策樹和回溯過程兩個部分。這題的決策樹的深度等於輸入數字的長度。它的第0層代表第一個數字的選擇（例如 2 -> a, b, c），第1層代表第二個數字的選擇（例如 3 -> d, e, f），以此類推。
樹的葉子節點（完成所有數字的選擇時）就是一個完整的字母組合。
接著講下回溯過程，首先是選擇（Choose）：在當前處理的數字所對應的字母中，選擇一個字母加入當前的組合字串中，接著是探索（Explore）：遞迴地呼叫回溯函式，處理下一個數字，最後是回溯（Unchoose/Backtrack）：當遞迴呼叫返回後，需要撤銷剛剛的選擇（例如從組合字串中移除這個字母），這樣才能讓迴圈繼續，嘗試這個數字對應的其他字母，回到上一個狀態。

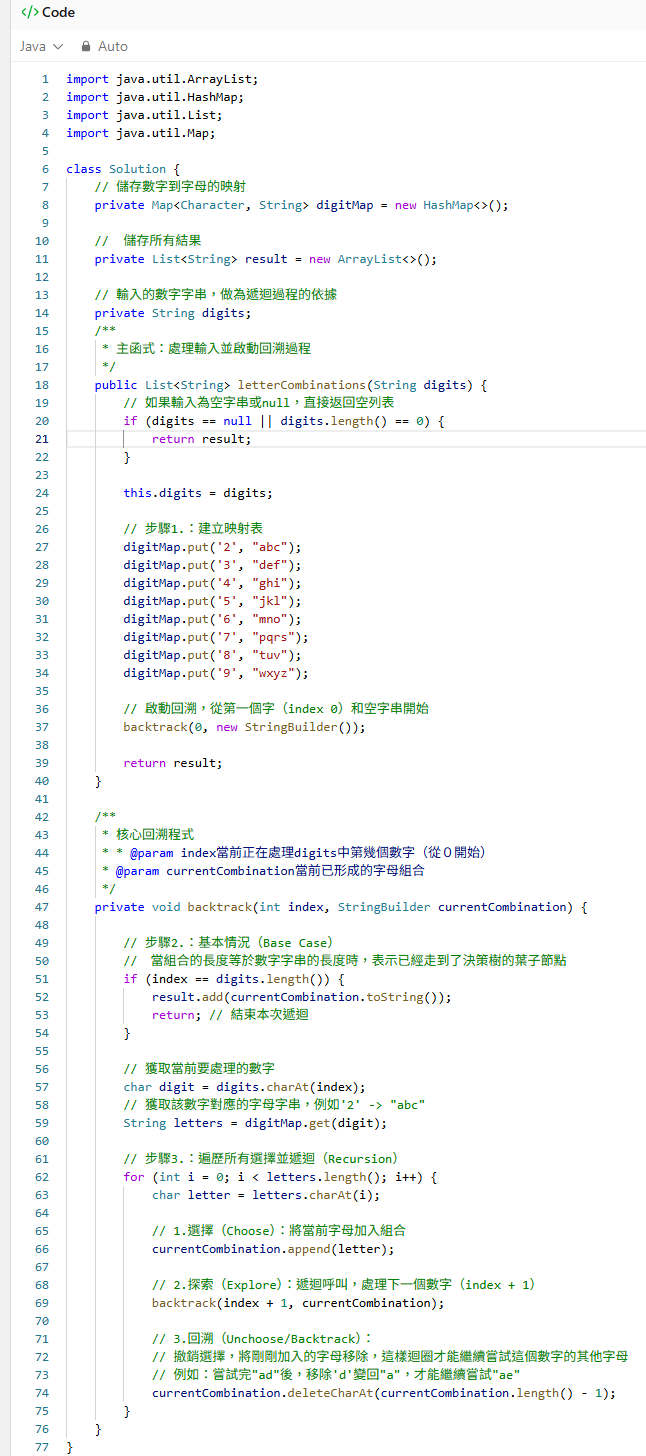
這題的解題步驟分成三部分，首先建立映射（Mapping）：準備一個資料結構（例如Hashmap或陣列）來儲存2 - 9每個數字與其對應字母的關係。
接著是基本情況（Base Case）：如果當前組合的長度等於輸入數字字串的長度，這表示已經完成了一個完整的組合。將這個組合加入結果列表，然後返回。
最後就是遞迴（Recursion）：先取出當前要處理的數字，接著遍歷該數字所對應的所有字母，對於每個字母：將字母加入當前組合，遞迴呼叫回溯函式，處理下一個數字，對當前組合中移除該字母（回溯），以便嘗試下一個選擇。在這裡，遞迴看起來就是回溯過程。