28. Find the Index of the First Occurrence in a String
    這題是字串搜尋問題，目標是找到子字串（needle）在主字串（haystack）中第一次出現的起始索引。如果主字串中找不到子字串，則回傳 -1。
    這題的本質是執行一個子字串搜尋演算法。由於題目對效率沒有極高的要求（限制條件中字串長度 L ≤ 10^4），所以可以從最直觀的暴力解法（Brute Force）開始。

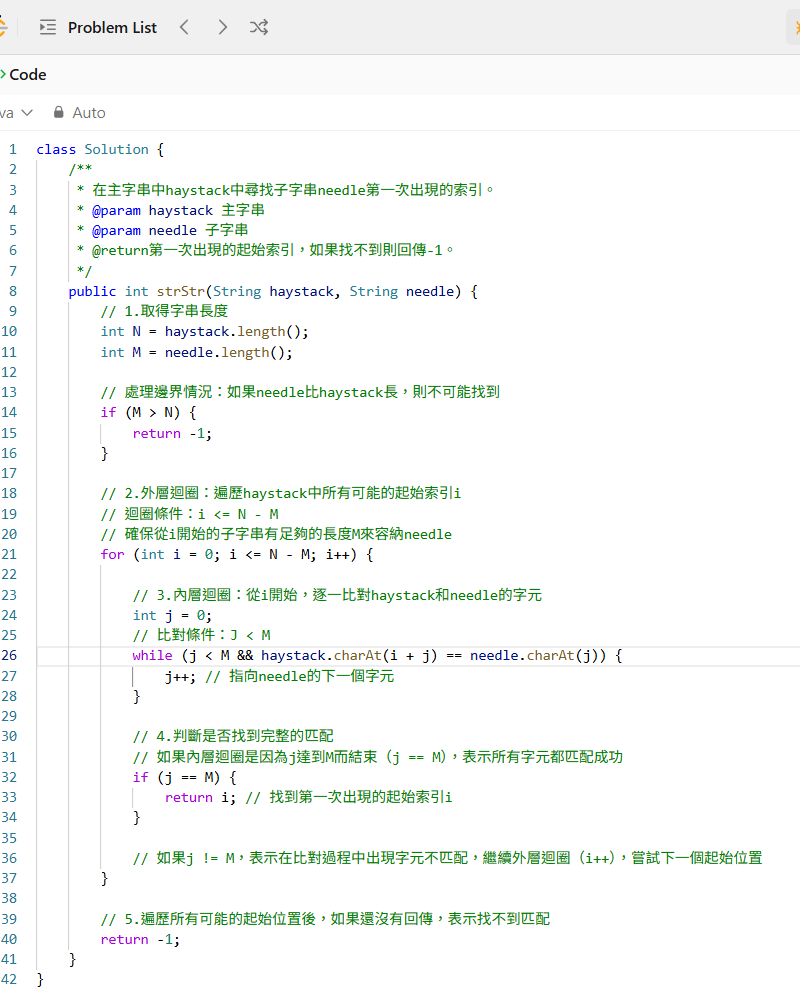
暴力解法的核心思想是：
從主字串haystack的第一個字元開始，嘗試將子字串needle放在這裡進行逐一比對。如果比對成功，立即回傳當前的起始索引；如果比對失敗，則將needle的起始位置向後移動一位（從haystack的第二個字元開始），重複上面步驟。
接著，持續這個過程，直到haystack中剩下的字元數量不足以容納needle為止。
如果整個過程都沒有找到匹配，則回傳 −1。

複雜度分析
時間複雜度 (Time Complexity)：在最差情況下（例如haystack = "aaaaab", needle = "aab"），需要對haystack的每個起始位置都進行幾乎完整的needle長度次比對。
假設 haystack 長度為N，needle 長度為M。
外層迴圈（遍歷起始位置）最多執行N – M + 1 次。
內層迴圈（逐一字元比對）最多執行M次。
因此，時間複雜度為O((N – M + 1)⋅M) ≈ O(NM)。對於N , M ≤ 10^4
的約束條件來說，這個解法是可接受的。