前幾天我盤算在 鐵人賽 打下面的方程式,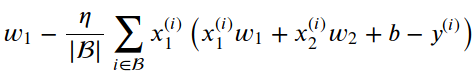
我用 『加入數學公式』
w_1 - \frac{\eta}{|\mathcal{B}|}
\sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b -
y^{(i)}
%7D%20%5Cleft(x_1%5E%7B(i)%7D%20w_1%20%2B%20x_2%5E%7B(i)%7D%20w_2%20%2B%20b%20-%20y%5E%7B(i)%7D)
結果就是一串上面 URL Link。我知道簡單的方程式如下方,是可以的。是我用的語法錯誤嗎??
w_1 -
\frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}} \frac{ \partial
\ell^{(i)}(w_1, w_2, b) }{\partial w_1}
可以出現

我沒用過,
如果是我的話我會在Word編輯好貼圖上來 @@
好的 謝謝,我現在遇到複雜的公式也是類似的方法: 先到其他地方編輯好,剪貼圖上傳
我是覺得這只是個工具,
我比較重視花比較少時間達成一樣的效果,
如果沒有絕對必要用語法寫,
Word編輯還比較快比較直觀...
當然如果你語法寫很快是沒差.
可以先在這邊打公式:
https://www.mathjax.org/#demo
(用兩個錢字號包起來的地方是公式)
打習慣有時會覺得比按編輯器還快
你最後少一個)
w_1 - \frac{\eta}{|\mathcal{B}|}
\sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b -
y^{(i)} )
測試 \displaystyle 能不能讓公式大一點
\displaystyle w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)} \right)
試過了 \displaystyle 感覺還變小呢! 我也希望把他放大,有方法嗎?
我剛剛看 google 的文件
有 chs 參數可以指定大小
例如像我上面那樣...
我剛剛終於有測試 在 URL 加上 『chs=???x???&』
對我個人來講,感覺還蠻難調的。不過算是可以解決問題。
w_1 - \frac{\eta}{|\mathcal{B}|}
\sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b -
y^{(i)}\right)