以前沒寫過如此複雜的數學公式,所以想請教各位,這裡似乎不能上傳檔案,我把需要的公式貼上來,若有疑問在告訴我,謝謝

題目:

生成出??與??後，GEE估計法分別採用Indep進行參數估計並重複模擬過程100次

以下是生成數據:
import numpy as np

np.random.seed(100)

X1 = np.random.normal(0,1,size = (200,3))
X2 = np.random.uniform(0,2,size =(200,3))
#X = np.hstack(( X1[:,np.newaxis], X2[:,np.newaxis]))#合併為200列2行

mu = 1 + 0.5X1 - 0.5X2 # 200列 3行
sigma = np.array([[1,0.5,0.25],[0.5,1,0.5],[0.25,0.5,1]])
Y = np.random.multivariate_normal(mean=mu.mean(axis=0), cov=sigma, size = 200) #mu.mean(axis=0)是把每一行的mu相加，有3個值

mu.shape,Y.shape

公式(用到的公式):
V 是一個 n*n的變異數矩陣

初始化 D_partial_beta

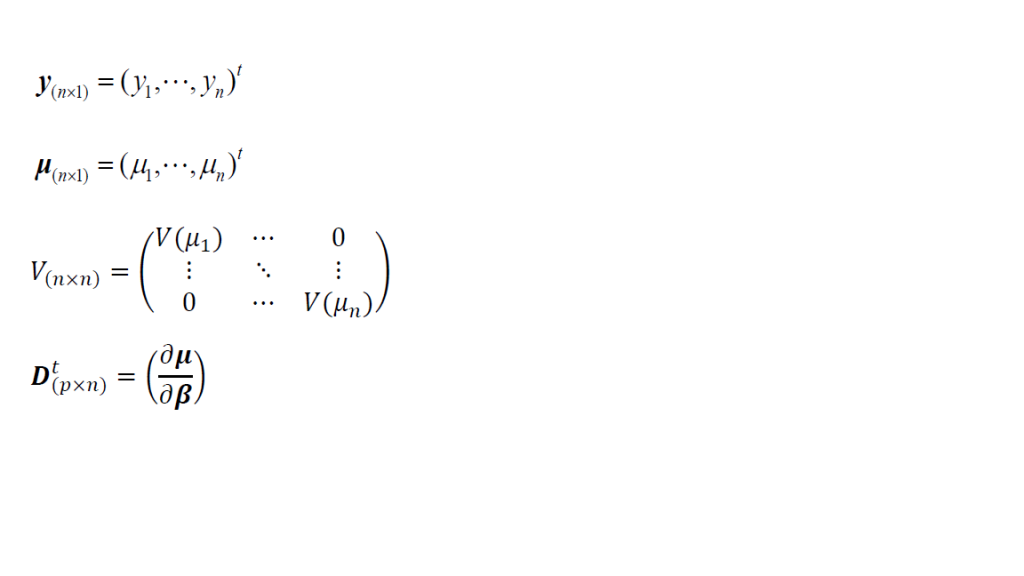
D_partial_beta = np.zeros((200, 3))

每一行 i， mu_i 對 beta 的偏導數

for i in range(200):
mu_i = mu[i, :]
D_partial_beta[i, 0] = mu_i[0] # mu_i 對 beta_0 的偏導數
D_partial_beta[i, 1] = mu_i[1] # mu_i 對 beta_1 的偏導數
D_partial_beta[i, 2] = mu_i[2] # mu_i 對 beta_2 的偏導數

D_t = D_partial_beta.T
D = D_partial_beta

D_t.shape,D.shape

計算 V(mu_ij)

mu_mean = np.mean(mu)
mu_centered = mu - mu_mean
mu_centered_T = mu_centered.T
#print(mu_centered_T.shape)
mu_cov = np.dot(mu_centered, mu_centered_T)/200
Var_mu = mu_cov
V = Var_mu
V.shape

計算 A = Diag(V(mu_ij))

A = np.diag(V)
A = np.diag(A)
#print("D(V(mu_ij)) = \n", D_V)
R = np.eye(200) # 這裡R(a)用1 0 0 1 那種衡等矩陣即可

計算 A 的特徵值和特徵向量

eigenvalues, eigenvectors = np.linalg.eig(A)

取特徵值的平方根

sqrt_eigenvalues = np.sqrt(eigenvalues)

構造對角矩陣

Lambda_sqrt = np.diag(sqrt_eigenvalues)

計算 A 的平方根

A_sqrt = np.dot(eigenvectors, np.dot(Lambda_sqrt, np.linalg.inv(eigenvectors)))

#print(A_sqrt.shape)

計算V(alpha)

V_alpha = np.dot(A_sqrt,np.dot(R,A_sqrt))
V_alpha.shape

result_array = np.zeros((200, 3, 3)) # 200x3x3
V = V_alpha

for i in range(200):
Di = D[i,:]
Di_t = Di.T
Vi = V[i,i]
D_V_D = np.dot(Di_t, np.dot(Vi, Di))
result_array[i] = D_V_D

D_V_inv_D = result_array
#print(D_V_inv_D.shape)
sum_D_V_inv_D = np.sum(D_V_inv_D,axis = 0)
inv_sum_D_V_inv_D = np.linalg.pinv(sum_D_V_inv_D)
#print(sum_D_V_inv_D.shape)

result_array = np.zeros((200, 3, 3)) # 200x3x3

for i in range(200):
Di = D[i,:]
Di_t = Di.T
Vi = V[i,i]
res = Y[i,:] - mu[i,:]
D_V_inv_res = np.dot(Di_t,np.dot(Vi,res))
result_array[i] = D_V_inv_res

D_V_inv_res = result_array
#print(D_V_inv_res.shape)
sum_D_V_inv_res = np.sum(D_V_inv_res,axis = 0)
print(sum_D_V_inv_res.shape)

belta = np.ones((3,3))
max_iter = 100
eps = 1e-3

迭代 belta

for i in range(max_iter):

# 更新 [D^T V^(-1) D]^(-1)D^T V^(-1) (Y - mu)
update = np.dot(inv_sum_D_V_inv_D,sum_D_V_inv_res)

# 更新 belta
belta  +=   update

# 收斂
if np.max(np.abs(update)) < eps:
    break

得到最终的 belta 值

beta = belta[:, 0]

打印输出 beta

print(beta)

結果應該要和前面設的beta=[1,0.5-0.5]差不多,但我的結果感覺就錯的,所以我想請問我的問題在哪?謝謝