在演算法中, 有一個很重要的就是 Big O, 甚麼是 Big O 呢? 大家可以去查查 wiki, 我在這邊稍微解釋一下, 就是你這個演算法, 因為資料量的增加, 而計算的次數增加的狀況...

而 Big O 有那些呢, 我從 wiki 直接 image capture 一個表給大家看..

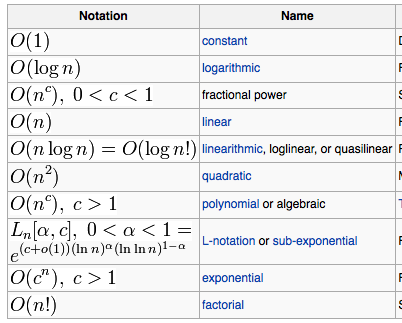
當然我們都知道, 越上面的話, 就資料量越多的話, 增加的也越慢, 相對的也越快, 而以 O(n log n) 作分界點, 以上通常是可以計算的, 相對的以下 O(n^2) 的幾乎是不能計算的..

與其說不能計算, 還不如說若是前題是 "資料探勘必然要有足夠大量的計算才有效" 話, 若這個資料量是幾百萬或幾千萬, 程式一跑一定無法在既定的時間滿足要求, 就像是須要兩天才能預測明天一樣, 一點意義也沒有, 所以在規劃資料探勘的可行性時, 一定要有能力去找出可計算的演算法才行...

當然要找到 O(1) 定數的計算不太可能, 若是在 O(n) 也算是幸運, 而是 O(log n!) 的話就是相對合理的, 而有些演算法本來就很難降低到 O (log n!) 的, 尤其是大家常在書上看到的 "基因演算法", 等等..

在 Clustering 的群落分析法, 書上的演算法也是 O(n^2) 以上, 若不是已經設定要計算幾個 Group 而用逼進法, 這也是一個幾乎不能計算的東西, 甚至大部份的演算法都是 O(n!), 就是 factorial 到 exponential 的演算法, 你可以直接略過書上寫的程式, 直接了解這情型是用在那種該場合就好.

因此為甚麼我花了好多年, 要找出一個好 Big O 的演算法來去算關聯分析, 以及把 Clustering Analysis 弄成可以算, 這是成功與失敗的關鍵.

而在 Data Mining 中, 的確演算法是占最重要的決勝點, 而 Big O 又是其關鍵, 因此在做演算法的調整中, 或者是找出那段程式碼是被執行最多次而造成影響的, 所須要的就是這些了....

嗯, 我的文章很少連結, 也很少有圖, 這算是破例嗎? 呵~~