神奇的Gray Code可是在1940年就研究出來,用來在PCM (Pusle Code Modulation)方法傳送訊號時避免錯誤,Gray Code可是有專利保護的喔~~
用Javascript征服演算法 (2-Gray Code)
產生Gray Code程式碼
其實這個題目有點私心,因為看了Gray code與幾何之間的對應關係如此奇妙後,就想來實做看看XDDD
何謂Gray Code?
Gray Code是一個數列集合,每個數都是由0和1的組成來表示,而每個相鄰由0和1組成的數之間,都只會有一個位元不同,舉例來說,如果是2位元的Gray Code,那就是 [00,01,11,10],而透過循環排列或是用反過來的順序寫,也會得到一組Gray Code, 像是 [01,11,10,00]也是一組Gray Code,但其實只是將第一個元素移到最後而已
而Gray Code與幾何之間的關係是這樣的,2位元的Gray Code的其中一集合式[00,01,11,10],而這可以對應成一個平面,如下圖所示,因此3位元的Gray Code就能夠對應成立方體,十分有趣阿XD,沿著邊界走不重複的話,每一條邊界都走過後,回到原點就剛好形成一組Gray Code,不同出發點就可以得到不同組的Gray Code欸XDDDD,超級能夠結合圖像的啦XDDD
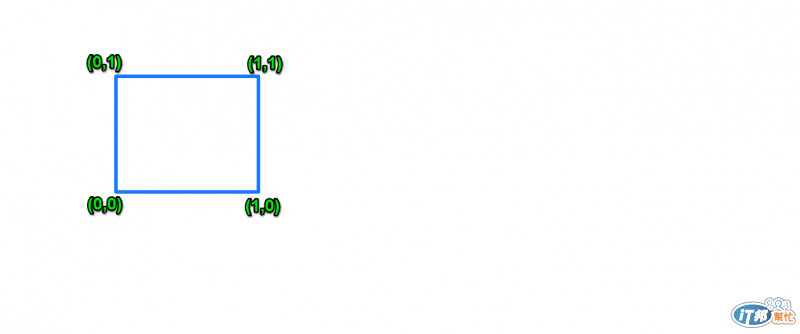
咳咳,有點過high克制一下XD 在了解Gray Code的定義之後, 我們就來觀察如何產生n位元的Gray Code, 由上述可知,n位元的所有Gray Code,其實都是透過所產生出的第一組Gray Code之後,藉由循環排列或是反過來寫就可以得到n位元Gray Code的其他組合集合,所以主要我們必須來觀察如何產生出n位元的第一組Gray Code
以下介紹兩種觀察出來的解法(一個較為簡單,但不容易利用程式碼建構出來,一個較難觀察出來,但卻容易去用架構程式碼)
第一種解法如下圖
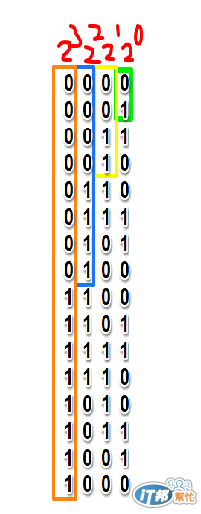
透過觀察可發現,由右側開始往左側來觀察,最右邊就是01 -> 10 -> 01 這樣遞迴的轉換,而右側數來第二列,就是由0011->1100->0011如此遞迴下去,依此類推,而究竟要多少開始由0轉換成1? 最右側可看見上方有個2的0次方,及表示最右側的遞迴從第2的0次方開始(也就是1)就要轉換成1,而右側數來第二列,就表示從2的1次方開始(也就是2)就要轉成1,也就是00後就要轉換成11,而後就重複11再轉換成00 如此不斷下去。
以上為第一個解法,假設要求n個bit的Gray Code, 那可以先求n-1個bit的Gray Code然後在每個元素的左邊加上0,而後再將n-1個bit的Gray Code顛倒放,然後在左邊加上1,以2個bit的Gray code為例
[0,1] //(2-1) bit的gray code
//因此先將1 bit的gray code直式放在最右側
0
1
//之後再左邊加上0
0 0
0 1
//而後在顛倒順序,並在左側加上1
0 0
0 1
1 1
1 0
第二種解法
接下來這解法就是透過觀察奇偶項來得到統一的解法
由下圖我們來將轉換的位數記錄起來,由 0000 轉換成 0001是由右邊數來第1位改變,依此類推,我們將會歸納出下圖結果
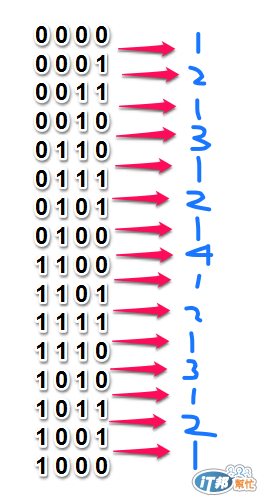
可以發現奇數傳變成下一列時都是為1,表示都是最右邊那一位數從0變成1或者從1變成0,那偶數列轉變成下一列呢呢,從觀察上一列變成下一列的變化中,可發現,偶數列的位數變化,是從上一列最右邊數過來為1的位數的左邊那個位數的來轉變的,如第四列變成第五列(0010->0110)是由右邊數來第二位的左邊那位數由0變成1而產生出0110的
由上述觀察可以歸納出一個判斷奇偶列就能算出Gray Code的方式,奇數列要變成下一列就是把最右邊那一位數轉變成1或0,而偶數列就是觀察本身最右邊的1為哪一位數,那下一列肯定就是那一位數左邊的數字由0變成1或1變成0啦
以上是今天的Gray Code介紹,不知道大家比較喜歡哪一個解法呢0.0~~~![]()

試著實作第一種解法,其實不會很難架構程式,這個解法既然想法上已經是比較直接簡單了,通常做起來也就不會太難,做出來後倒是發現,效能上不夠好,會是O(n*2^n), 這還頗糟。
不曉得第二種解法的big O是多少就是了,是一定都要掃過2^n列,但每一次做的時候,只要判斷是奇偶跟最右邊的1的位置,不需掃完一整列的code,這方面光這樣想起來效率上應該就比第一種來得好很多了。
小賴真是認真~~等我寫完鐵人再來跟你討論兒~
不過我直覺也是認為第二種解法的複雜度應該較低就是了![]()
我當初是覺得第一種解法要用到的更改方式相對繁瑣很多,就有點抗拒去寫它XDDD
XDD 沒辦法,喜歡跟你討論演算法
另外請教一個問題,gray code有什麼實際上的用途嗎? 謝謝。