Quick Sort~Sort如期名，快來看看他多快吧!!!!
今天要來介紹公認在某些case下，使用此排序法速度是最快的，那就是Quick Sort

Quick Sort主要是使用了Divide and Conquer的觀念，什麼是divide and conquer的觀念呢，那就是將大問題切割成小問題，等解決小問題之後，大問題也就解決了，如果小問題依舊很難，那就在切割成更小的問題，就能依序擊破，最後就能解決原本的大問題了

因此，Quick Sort在排序時，會選一個pivot的值，與其比較後，形成一段都比pivot小的集合與一段都比pivot大的集合，最後再將pivot放置奇中央，這樣就完成了divide得的動作，而conquer得部分，就是將小集合與大集合中間放置pivot後，再將小集合與大集合視為獨立的集合，在進行quick sort排序，如此一來，最後就能完成排序

一般而言,會說quick sort會是最快速排序法，是因為多數情況下可以獲得很好的效率，而為什麼多數情況下quick sort都能有比較好得效率?我想是因為他將排序切割成小的問題後，在解決小問題時，很有可能選中的pivot剛好就是能將小集合與大集合元素的個數左右相同的pivot，兩邊元素個數一樣，代表小問題的元素不會太多，那這樣就容易一下就排序完成

因此由上述可知，對quick sort來說，如何去選取pivot很可能就會影響整體的排序效率，而一般在書上可以見得的選取方式，最普通的就是直接選取數列開頭的元素當作pivot，之後就能分出一集合都比pivot小的元素集合，而另外一側則是都比pivot大的集合(如圖)

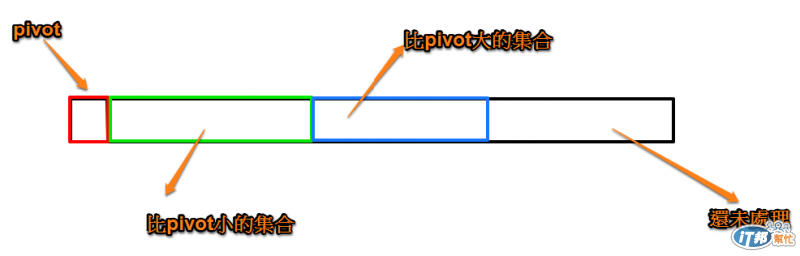
而此實作的方式大致上就是

1. 設定變數i由左到右掃描，直到找到比pivot大的值
2. 設定變數j由右到左掃描, 直到找到比pivot小的值
3. 將i與j所對定的陣列值交換
4. 如果i > j則表示排序已完成
5. 將pivot所在陣列值與i-1所在陣列值互換
6. 將左右兩側陣列在作遞迴排序

在此特別要介紹一下在演算法聖經Introduction to Algorithms中所計載的方式

以下為書上計載的pseudo code

QUICKSORT(A, p, r) 
   if p < r 
     then q <- PARTITION(A, p, r) 
               QUICKSORT(A, p, q-1) 
               QUICKSORT(A, q+1, r) 
end QUICKSORT 

PARTITION(A, p, r) 
    x <- A[r] 
    i <- p-1 
    for j <- p to r-1 
        do if A[j] <= x 
                 then  i <- i+1 
                         exchange A[i]<->A[j] 
    exchange A[i+1]<->A[r] 
    return i+1 
end PARTITION  

此方法中，是透過選取數列最後一項(或最左邊)為pivot的值，而i與j都會同時往右的方式去尋找出比pivot小集合與比pivot大的集合

上述方法可以大概去想像，i就是比pivot小的集合指標，j呢就是往右不斷尋找陣列值的變數，因此可以想見，只有在j所在的陣列值比pivot小的時候，我的i旗標才需要往右前進，表示又有一個元素是屬於比pivot小的集合裡囉

以下為實際運作pseudo code的演譯

完成後

此方法之所以有名，似乎是因為他pivot的選取方式，能夠使得pivot左右兩邊的小集合經常都能分布平均的個數，但這部分我仍舊不太清楚為何? 可能要在查查資料，希望明天可以進一步解釋

以上就是quick sort的介紹，下一篇就來實作看看吧，初次看或很久沒看quick sort都會有點難進入狀況，但我上圖的演繹應該可以讓各位初學或者複習者更快進入狀況: )

下一篇GOGO~~