上一篇作出了一個基本的Random Walks的物件，並讓它在螢幕上動起來，但只有實現了往四個方向，上、下、左、右，但螢幕上每個像素都有八個相鄰的像素，如下圖

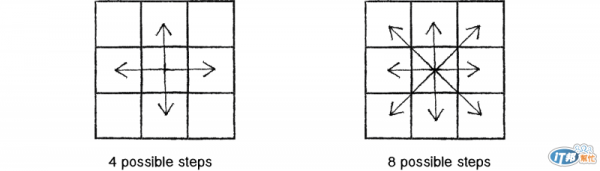
有八個方向可以移動，加上原地不動就有九個可選的方向，所以我們可以將原本的Random Walks做一些改進。

將X與Y軸拆開來看的話，X軸的移動有3個選擇，往左移動1個像素、不動、往右移動1個像素，Y軸同樣有3個選擇，計算X與Y軸的所有組合，剛剛好就是9種，依照這個想法，作出如下改進

step(){
  stepx = int(random(3)) - 1; //可能產生 -1, 0 or 1
  stepy = int(random(3)) - 1;
  x += stepx;
  y += stepy;
}

或者也可以改成使用浮點數，random(-1, 1)會產生由-1.0 ~ 1.0的任意隨機數值

void step() {
  float stepx = random(-1, 1);
  float stepy = random(-1, 1);
  x += stepx;
  y += stepy;
}

包括上一篇與這一篇，關於Random walks的變化與改進，要說明的只是機率這件事，Walker往任何方向走的機率都是一樣的，4個方向，任何一個方向的機率是 25% (1/4)，9個方向則是 11.1% (1/9)

這可以解釋random()這個方法在Processing中的運作方式，稱為均勻分佈(Uniform Distribution)，在範圍內每個值出現的機率相等。書中有一個範例去做驗證，

網址在此 http://natureofcode.com/book/introduction/#canvas1

int[] randomCounts;

void setup() {
  size(640,240);
  randomCounts = new int[20];
}

void draw() {
  background(255);

  // Pick a random number and increase the count.
  int index = int(random(randomCounts.length));
  randomCounts[index]++;

  stroke(0);
  fill(175);
  int w = width/randomCounts.length;
  // Graphing the results
  for (int x = 0; x < randomCounts.length; x++) {
    rect(x*w,height-randomCounts[x],w-1,randomCounts[x]);
  }
}

可以看見個每個長條大致上會平均增長，雖然長條之間會有細微的偏差，但隨著時間會越來越平均。

下一篇會介紹非均勻分佈(Non-Uniform Distributions)，當粒子在空氣中運動的時候，雖然是隨機運動，但卻可能因為風的影響而趨向往某個方向移動，那要如何模擬這個情況呢？