雖然說修讀原因在我定義是這系列文章的重點, 但話說演算法這門課應該沒有人懷疑為甚麼要修習吧?
只是應該有人發現目前課的安排是:
這樣的重覆, 而演算法到底算是電腦技術, 還是數學統計呢? 這是一個非常好的問題. 在 wiki 是這樣寫的:
"在數學和計算機科學/算學之中,演算法/算則法(Algorithm)爲一個計算的具體步驟,常用於計算、資料處理和自動推理。精確而言,演算法是一個表示爲有限長[1]列表的有效方法。演算法應包含清晰定義的指令[2]用於計算函式[3] 。"
在這邊有一個很有趣的問題, 就是 "有限長", 這這是在 1970 年代的定義, 認為有限長的是為 Algorithm, 而無限的就是 Computing Method, 而在限在的資料運算, 即使面對有限的步驟, 但面對源源不絕沒有止盡的資料是沒有計算的終點, 雖然說最後也可能是種 "Infinite Loop/無限迴圈", 但最後還是在既定的步驟.
但拉回來, 所有的計算都是種演算法, 甚至是某些公式本質就是種演算法的表示, 學習演算法說穿了就是學習找到答案方法的步驟, 然後去執行, 所以這在某方面是種最基礎也是種最終的學習科目之一.

在學演算法時, 最重要的是如何找到解的方法, 在之前可以去想如何分類演算法.
由設計模式來分:
透過上面這幾種思維, 幾乎是可以解決 95% 以上的問題, 再透過下面幾個方法:
就可以將之實作, 只是接下來有一個很大的問題, 就是演算法的分析, 演算法分析就是去分析一個演算法在執行所須的資源, 以及要付出的代價, 其中最後的它的效率, 此時就會帶出演算法最重要的觀念, Big O, 也就是下表:

此時就有一個很重要的名詞, 就是 NP-Complete/NP-Hard, 也就是 "非定常多項式 / non-deterministic polynomial), 這不只是在演算法很重要的一件事, 更重要的在 Big Data 的計算中, 演算法的重要不只在於 NP, 也包含在 Big O 後面的量值.
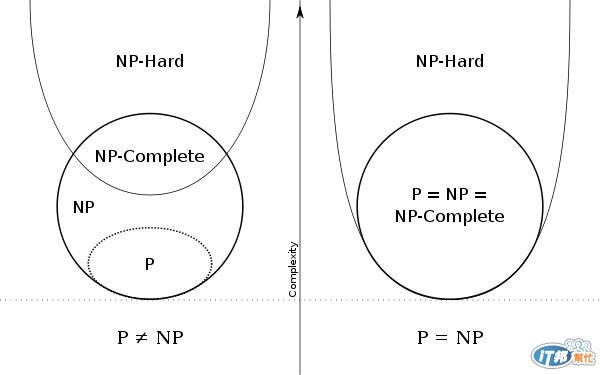
當然很多解不是不存在, 而是適用的方法與範圍是有限的, 不然只是沒想到而已, 而演算是門可以放在大學, 研究所或博士後研究的科目, 就可以知道這門課所須要的基礎與博大精深.
電子書:
開放課程:
關鍵字:
