**題目來源：**Maximum Depth of Binary Tree

問題：
給予一棵[二元樹][BinaryTree]，試著找出他的最大深度。

// 題目對於二元樹的定義
public class TreeNode {
   int val;
   TreeNode left;
   TreeNode right;
   TreeNode(int x) { val = x; }
}

例子
所謂二元樹的深度就是從 根節點(root) 到 葉節點(leaf) 的距離。 (沒有子節點的節點稱做葉節點)

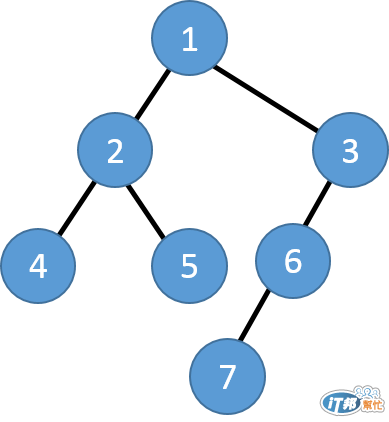
他的最大深度就是 4, 因為在所有的路徑當中從 1 到 7 號節點的距離最遠，有四個節點。

想法
關於最大深度，我們需要的是計算所有路徑的深度，然後再從這些深度中找出一個最大的即可。
所以我們需要兩個 Stack ，一個是存放 目前走訪的路徑，另一個是 暫存著我們尚未走訪的路徑。

當存放的我們 目前走訪的路徑 stack 到達 葉節點 時，我們就可以將此 stack 的 size 與目前的最大深度相比較 再將較大的那一個設定成 目前最大深度。依此類推，每走到一個葉節點，就可以比較目前的最大深度是否為最大，直到走完所有的路徑（也就是 暫存路徑的 stack 為空) 時，就可以得到最大深度了。

虛擬碼

建立一個 remainPathStack (暫存路徑)
建立一個 currentPathStack (目前走訪路徑)
Push 'root' to remainPathStack
while remainPathStack is not empty:
    currentNode = remainPathStack.peek
    if (currentPathStack is no empty AND currentPathStack.Peek == remainPathSTack.Peek):
        if currentPathStack 的 size 大於 MaxDepth:
            將 MaxDepth 設定成 currentPathSizeStack's size
        pop one node from currentPathStack
        pop one node from remainPathStack
    else:
        push 'currentNode' to currentPathStack
        if node has left child:
            push 'left child' to remainPathStack
        if node has right child:
            push 'right child' to remainPathStack

• 如果你用 C＃ 可以利用我的 測試程式 來驗證

• 如果你用 Java or Python or C++ 可上 LeetCode Online Judge 驗證

  // 我的解法 C# 版本
  public int CalculateMaxDepth(TreeNode root)
  {
  int maxDepth = 0;

   if (root == null)
       return maxDepth;
  
   Stack<TreeNode> remainPathStack = new Stack<TreeNode>();
   Stack<TreeNode> currentPathStack = new Stack<TreeNode>();
  
   remainPathStack.Push(root);
  
   TreeNode node;
   while (remainPathStack.Count != 0)
   {
       node = remainPathStack.Peek();
  
       if (currentPathStack.Count != 0 && node == currentPathStack.Peek())
       {
           if (currentPathStack.Count > maxDepth)
               maxDepth = currentPathStack.Count;
           remainPathStack.Pop();
           currentPathStack.Pop();
       }
       else
       {
           currentPathStack.Push(node);
           if (node.left != null)
               remainPathStack.Push(node.left);
           if (node.right != null)
               remainPathStack.Push(node.right);
       }
   }
  
   return maxDepth;
  

  }

來做一點點小小的 refactor 吧，讓程式碼更加友善，雖然有點過頭，但也挺有趣的，不是嗎？讓程式碼像文章一樣！

// 有點重構過頭的 C＃ 版本
public int CalculateMaxDepth(TreeNode root)
{
    int maxDepth = 0;

    if (root == null)
        return maxDepth;

    Stack<TreeNode> remainPathStack = new Stack<TreeNode>();
    Stack<TreeNode> currentPathStack = new Stack<TreeNode>();

    remainPathStack.Push(root);

    TreeNode node;
    while (IsNotEmpty(remainPathStack))
    {
        node = remainPathStack.Peek();

        if (IsCurrentPathDownToLeafOrOnBackWay(currentPathStack, node))
        {
            if (currentPathStack.Count > maxDepth)
                maxDepth = currentPathStack.Count;
            remainPathStack.Pop();
            currentPathStack.Pop();
        }
        else
        {
            currentPathStack.Push(node);
            if (node.left != null)
                remainPathStack.Push(node.left);
            if (node.right != null)
                remainPathStack.Push(node.right);
        }
    }

    return maxDepth;
}

private static bool IsNotEmpty(Stack<TreeNode> currentPathStack)
{
    return currentPathStack.Count != 0;
}

private static bool IsCurrentPathDownToLeafOrOnBackWay(Stack<TreeNode> currentPathStack, TreeNode node)
{
    // 因為當目前的節點沒有任何子節點時， remainPathStack 就不會 push 節點進去
    // 此時，remainPathStack 的 peek 會和 currentPathStack 的 peek 相同
    if (currentPathStack.Count == 0)
        return false;
    return node == currentPathStack.Peek();
}