前一篇提到加法器的效能計算，就其原因主要就是高位運算必須等待低位的進位輸出信號

那是否可以提前計算出這些進位輸出信號以提升效能呢

那麼我們就來分析一下進位輸出信號的計算過程：

第一行是說只要 Ai、Bi、Ci 任兩個是一，則進位自然就會是一，經過提出 C 之後變成下面的算試

再來因為 Ai 和 Bi 是在一開始就可以知道的，因此我們再設兩個變數 Gi、Pi 來代表 Ai * Bi 、 Ai + Bi

通過這樣通用的表達式，我們就可以分別推導出 Ci+1 是多少：

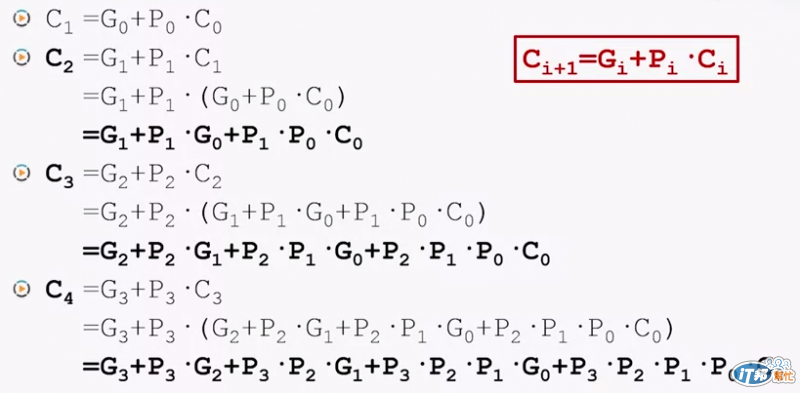
可以看到所有的數值都是在運算一開始就可以得到的數值，因此我們就不需要依賴前面的運算結果才能進行計算

那在電路上的實現就如下圖所示，我們以 C4 為例：

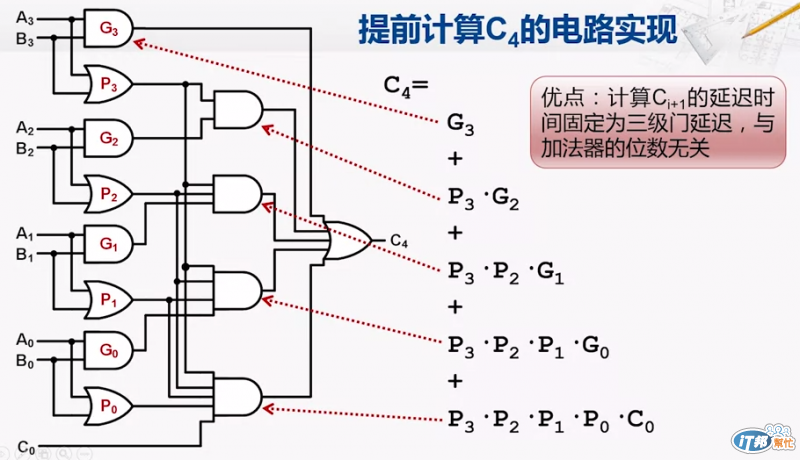
所以我們可以看到 C4 只需要 A&B 和 C0 就可以推算出來，而且只需要 3T 的時間

由此類推其實不論是多少的位數，所有的延遲時間都只要三級

由這種方式所構成的加法器就稱為 超前進位加法器 (Carry-Lookahead Adder CLA)

計算進位時需要 3T，但因位在全加器內部還需要 1T 的計算，所以總延遲時間就變成 4T

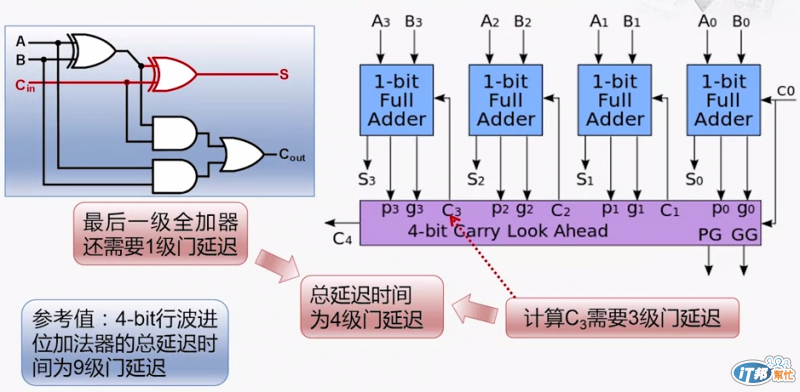
另外以 32bits 的加法器來說，原先需要 65T 的時間

如果採用完全的超前進位加法器只需要 4T，這樣一來效能的提升就變得十分可觀

但是事情沒有我們想的那麼美好，因為如果要實作完全的進位加法器

將需要 32輸入的 AND 和 OR 邏輯閘，造成電路過於複雜難以實現

因此通常折衷的實現方式是會多個小規模的超前進位加法器拼接而成

例如用 4個 8bits 的超前進位加法器連接成 32bits 的加法器

如此一來他的延遲時間就變成 13T 也就是 0.26ns，換算成頻率就是3.84GHz

至於為甚麼會是 13T 呢，就留給大家自己推算囉

如此一來加法器就不會成為 CPU 在設計時的關鍵路徑，那也就不會降低整個 CPU 的性能了