前面提到馬可夫蒙地卡羅法(MCMC)，感覺非常的神奇！
這個方法可以模擬目標分佈，並且做抽樣的動作，成為一個sampler！

怎麼做到的！

這邊我只講結論，如果看官需要理論的話可以參考Introduction to Markov Chain Monte Carlo

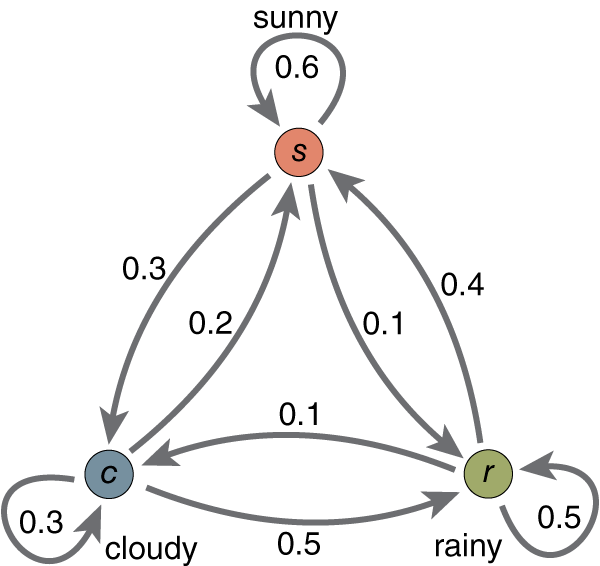
其實建立馬可夫鍊就是像上面看到的這張圖一樣的東西，每個點代表的是不同的狀態，狀態跟狀態之間有箭頭，箭頭代表的數字代表著有多少的機率會從這個狀態轉移到下一個狀態。
所以相對應的就是轉移矩陣，像下面這種東西。

他紀錄了每個狀態之間轉移的機率，既然談到機率，機率的分佈圖中X軸也可以視為一個狀態。

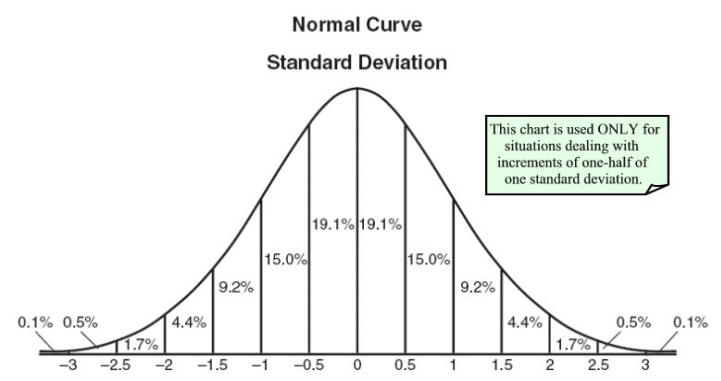
像以上是連續分佈，連續分佈的狀態是連續的數值。什麼！你說你沒看到狀態，不不不一定是眼睛業障重。那不然看看下面這張有沒有。

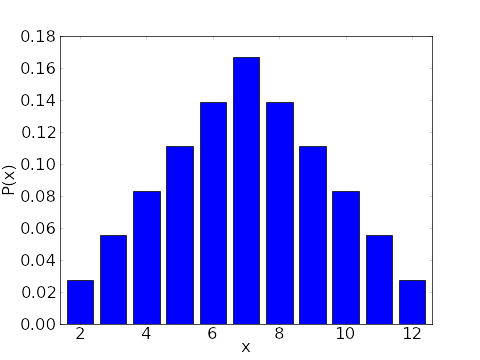
這邊就是離散的分佈，這個總有狀態的感覺了吧！對！也就是說馬可夫鍊這東西可以把狀態跟狀態之間的轉移關係學起來，學起來之後你可以讓他吐出來，吐出來的狀態序列仍然是遵循著原分佈圖的！
這就是馬可夫鍊一個好的性質！

Detailed balance

這個性質從哪來？從一個叫作detailed balance(細緻平衡)的性質來的，不過這邊不講公式，要找公式的話請左轉維基百科。
什麼叫作細緻平衡呢？也就是跟以前學到的化學平衡有點類似，概念就是流進等於流出，在這裡我們講的是對馬可夫鍊的每個狀態都要具有這樣的特性，所以這種馬可夫鍊被稱為可逆馬可夫鍊。
也就是當馬可夫鍊學習一個分佈的時候，他會漸漸收斂到那個分佈的樣子，當他已經收斂到狀態跟狀態之間的流入流出都相同，那也就代表學完了！

這邊還聽不懂的話可以參考：

1. Detailed Balance Explained To My Son
2. Equilibrium Means Detailed Balance

方法

有名的MCMC方法有幾種：

1. Metropolis-Hasting algorithm
2. Gibbs Sampler

我們在之後的實作當中，模擬退火法會用到的正是Metropolis-Hasting algorithm。