前言:影像處理是把數位的影像作前置的加工及處理,以便日後的分析。
人可以透過眼睛傳遞影像,並利用大腦的分析;而鏡頭就仿如人類的眼睛,當數位影像傳遞給電腦時,無時無刻也有機會產生雜訊,而且電腦在處理影像時並沒有人類大腦般聰明,因此需要影像處理,把雜訊濾掉、邊緣銳化...,把重要的影像轉換成電腦的角度,以便日後處理(影像處理完後,下一個課題是影像識別)
開發環境:C-Free 5
注: 1)以下只提供演算法程式,沒有提供main檔案
2)原始圖檔取自網路
================分格線================
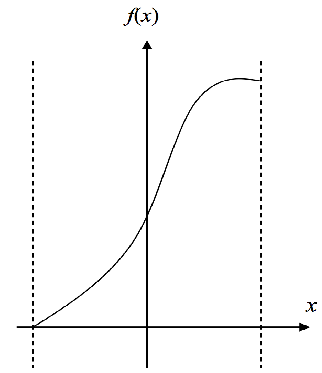
圖1)上圖為 影像原始影像
解釋:在圖1中,我們可以看出從負X 至 正X之間的f(x)為一個漸變層
在電腦視覺最喜歡瞬間變化的影像,相反而言,最害怕遇到漸變層的影像
舉個例子:1000度近視的人,沒有戴眼鏡所看到的東西,就仿如電腦所看到的視角,一片模模糊糊的;因此而要為電腦戴上眼鏡(影像處理),而是次所解說是用Laplacian微分法作處理。
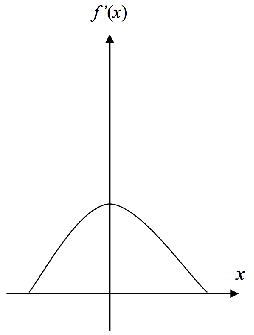
圖2)上圖為 經過1階Laplacian微分後的影像
解釋:我們可以透過圖2得知,1階微分後,f(x)由一個漸變層,變成近似脈衝的波形,而這個脈波就是影像中物體與物體或物體與背景的交界線。把整個影像所有的交界線勾晝出來,我們就可以對影像作後續的處理。
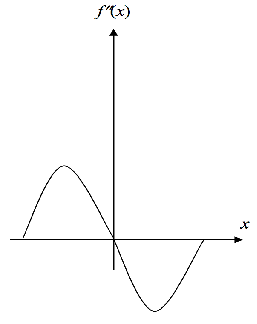
圖3)上圖為 經過2階Laplacian微分後的影像
解釋:2階微分處理後,f(x)會產生正負相反的脈波,而像素沒有比0更小的強度(灰階值中:0為黑色;255為白色)。此外,我們在數學公式中得知,脈波是無限的延伸,因此我們需要把超過255的像素,固定為255;把低於0的像素,固定為0。(我會稱作:收歛)(程式碼所處理的影像為RGB,bmp檔)
*一階對比二階而言,後者影像的強度會比前者為大,因此輸出影像的圖像邊界會銳化。(邊界會更明亮)
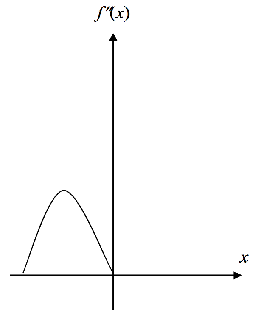
圖4)上圖為 經過2階Laplacian微分,並且經過收歛後的影像
====================分格線====================
void laplacian(unsigned char image_in[Y_SIZE][X_SIZE], unsigned char image_out[Y_SIZE][X_SIZE], double amp, int type){
int i, j, d;
int c[3][9] = { 0, -1, 0, -1, 4, -1, 0, -1, 0,
-1, -1, -1, -1, 8, -1, -1, -1, -1,
1, -2, 1, -2, 4, -2, 1, -2, 1 };
type = type - 1;
if (type < 0) type = 0;
if (type > 2) type = 2;
for (i = 1; i < Y_SIZE-1; i++) {
for (j = 1; j < X_SIZE-1; j++) {
d = c[type][0] * image_in[i-1][j-1] + c[type][1] * image_in[i-1][j ] + c[type][2] * image_in[i-1][j+1]
+ c[type][3] * image_in[i ][j-1] + c[type][4] * image_in[i ][j ] + c[type][5] * image_in[i ][j+1]
+ c[type][6] * image_in[i+1][j-1] + c[type][7] * image_in[i+1][j ] + c[type][8] * image_in[i+1][j+1];
d = (int)(d * amp) + OFFSET;
if (d < 0) d = 0;
if (d > 255) d = 255;
image_out[i][j] = (unsigned char)d;
以上為Laplacian 1至3階微分法的程式碼
=========================>程式解說<=========================
void laplacian(unsigned char image_in[Y_SIZE][X_SIZE], unsigned char image_out[Y_SIZE][X_SIZE], double amp, int type){
image_in[Y_SIZE][X_SIZE] //輸入影像的解析度&像素大小 (矩陣);輸入影像是利用矩陣的方式
image_out[Y_SIZE][X_SIZE] //輸出影像的解析度&像素大小 (矩陣);而輸出影像也是使用矩陣的方式
amp //輸出影像的像素放大率;在低階數或面對較暗沉影像時,我們可以透過放大像素的倍率,而達至影像更明亮的需求。
type //階數微分運算;決定影像需要幾階處理
int c[3][9] = { 0, -1, 0, -1, 4, -1, 0, -1, 0,
-1, -1, -1, -1, 8, -1, -1, -1, -1,
1, -2, 1, -2, 4, -2, 1, -2, 1 };
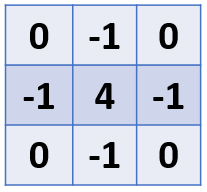
圖5)上圖為 Laplacian一階微分運算3x3的遮罩
圖6)上圖為 Laplacian二階微分運算3x3的遮罩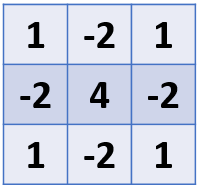
圖7)上圖為 Laplacian三階微分運算3x3的遮罩
*遮罩所產生方式,希望日後有機會詳細說明
type = type - 1;
if (type < 0) type = 0;
if (type > 2) type = 2;
type = type - 1; // 對應c[type][]的矩陣 矩陣是0~2;人是1~3;所以需要-1,由人的角度轉移至電腦角度
if (type < 0) type = 0; // 如果type小於0,type=0,防呆設計,防止超出範圍
if (type > 2) type = 2; // 如果type大於2,type=2,防呆設計,防止超出範圍
for (i = 1; i < Y_SIZE-1; i++) {
for (j = 1; j < X_SIZE-1; j++) {
for (j = 1; j < X_SIZE-1; j++) { //掃描輸入的影像,從第一行開始掃描 因為「3x3階數微分運算」是(X-1,Y-1)開始,所以i=1便可以 因為「階數微分運算」是(X+1,Y+1)結束,所以X_SIZE需要-1
for (i = 1; i < Y_SIZE-1; i++) { //掃描輸入的影像,每一行掃描結束後,往下一行再重新掃描 因為「3x3階數微分運算」是(X-1,Y-1)開始,所以i=1便可以 因為「階數微分運算」是(X+1,Y+1)結束,所以X_SIZE需要-1
d=c[type][0]*image_in[i-1][j-1] + c[type][1]*image_in[i-1][j ] + c[type][2]*image_in[i-1][j+1]
+ c[type][3]*image_in[i ][j-1] + c[type][4]*image_in[i ][j ] + c[type][5]*image_in[i ][j+1]
+ c[type][6]*image_in[i+1][j-1] + c[type][7]*image_in[i+1][j ] + c[type][8]*image_in[i+1][j+1];
此程式為「3x3階數微分運算的遮罩」對每一個輸入影像陣列作相乘,從而達到微分的效果。
d = (int)(d * amp) + OFFSET;
(int)(d * amp) //其中d變數為int(int為4 bytes) ; amp為double(double為8 bytes)
//d變數 x(乘) 放大倍數後,並轉換成int型態(收歛為整數,減少記憶體使用)
//d變數不會「四捨五入」
d = (int)(d * amp) + OFFSET; //計算結果 x(乘) 放大倍數 + 偏移量
//雖然我們可以用amp把輸出影像的像素以倍數方式放大;但OFFSET可以對像素作微量的調整。
if (d < 0) d = 0;
if (d > 255) d = 255;
在上文也提及到,在微化運算所產生的脈波,有機會超出0至255這個範圍,而且上段程式曾把「變數d作放大」,因此需要作出收歛。
if (d < 0) d = 0; //如果計算結果小於0 ,則d=0;
if (d > 255) d = 255; //如果計算結果大於255, 則d=255;
如果是筆者,我會直接修改程式直接用以下方法:
d = (unsigned char)d;
// unsigned char為1 bytes;範圍:0~255
//這樣也可以達到收歛的效果
image_out[i][j] = (unsigned char)d;
經過收歛後,資料型態需要更改(減少記憶體使用量)
(unsigned char)d; //unsigned char = 0~255
//原來d為int (32 bits)是多預留空間作運算
//經過收歛後便可轉換資料型態,減少記憶體使用量
image_out[i][j] = (unsigned char)d; //把新的強度(像素) 放在輸出端(陣列)
=========================>結果<=========================
圖8)上圖為原始影像 (圖片取自網路)

圖9) 上圖為 原始影像轉換為bmp檔案,把每一像素強度限制於0-255 (減少檔案佔用空間,但同時也令影像失去美感)

圖10) 上圖為 一階微分,放大1倍後影像

圖11) 上圖為 一階微分,放大5倍後影像

圖12) 上圖為 一階微分,放大20倍後影像

圖13) 上圖為 一階微分,放大100倍後影像

圖14) 上圖為 一階微分,放大2147483647倍後影像

圖15) 上圖為 二階微分,放大1倍後影像

圖16) 上圖為 二階微分,放大5倍後影像

圖17) 上圖為 二階微分,放大20倍後影像

圖18) 上圖為 二階微分,放大100倍後影像

圖19) 上圖為 三階微分,放大1倍後影像

圖20) 上圖為 三階微分,放大5倍後影像

圖21) 上圖為 三階微分,放大20倍後影像
===========================延伸===========================
!~!~!~!~!~!~!~!~!~!~!~!~! 問題一 !~!~!~!~!~!~!~!~!~!~!~!~!
問題: laplacian function中的amp(放大倍數),如果過度放大會影像會變得更暗沉。(見圖14:一階微分,放大2147483647倍後影像)
說明: 因為在運算過程中,每一像素的強度為int(即4個位元組數),如果超出最高位元組數,數值會變為負數,再存放至變數中。(見圖22: 超出資料類型之結果)
在int 32位元中,最高位元(第32位元)是用來控制正負數。
解決辦法1:在運算過程中把int改為long,提升位元組數。
解決辦法2:在運算過程中把int改為unsigned int,防止出現負數。
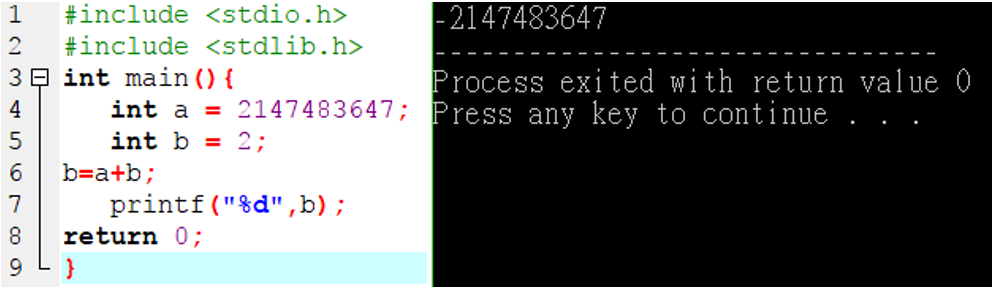
圖22) 上圖為 超出資料類型之結果
!~!~!~!~!~!~!~!~!~!~!~!~! 問題二 !~!~!~!~!~!~!~!~!~!~!~!~!
問題: 輸出影像放大倍率超過20後,運算過程只要不超過int的極限,輸出影像的亮度沒大改變。
解決辦法1:使用更高階數的Laplacian微分。在(圖12:一階微分,放大20倍後影像)與(圖17:二階微分,放大20倍後影像)中可以看出,放大倍數不變的情況下,愈高階數微分,在觀看上影像更明亮。
說明: 同時,我們可以從(圖2經過1階Laplacian微分後的影像)及(圖3 經過2階Laplacian微分後的影像)中的數學得知,在2階Laplacian微分後所產生的正負相反脈波,經過收歛後,像素強度雖然有機會與1階Laplacian微分一樣(同為255),但2階Laplacian微分負脈波收歛後,影像的黑白會產生強烈的對比,在視覺上顯得較明亮。
解決辦法2:利用OFFSET變數,為laplacian function產生偏移量,對影像的像素作調整。

所以看起來二階微分反而比較清楚?
對的,二階產生的邊界較分明
而且一階與二階,同樣是利用3x3遮罩方式,所以運算時間是一樣。