我記得老師說過，科技的研究大概往2個方向，不是最複雜化，就是最精簡化。
大家第一個學會的程式就是 hello world，而其次應該就是九九乘法表了
但大家有沒有想過九九乘法表，到底可以被我們搞得多複雜呢？

  int main(){
    for(int y=1;y<=9;y++){
      for(int x=1;x<=9;x++){
         printf("%d * %d=%d    ",y,x,y*x);
         }  }
return 0;
}

執行結果如下圖

======================分格======================

這應該是入門必學的程式了，但用這個去交作業，通常都會被老師打槍，要你去排版
這個時間就應該加一點\n (換行)、\t(TAB)
所以又產生了以下程式

int main(){
    for(int y=1;y<=9;y++){
      for(int x=1;x<=9;x++){
         printf("%d * %d=%d \n",y,x,y*x );
         }  }
return 0;
}

執行結果如下圖

======================分格======================

每完整輸出一句，均下一行。
這樣可不行，太長，所以要每9個才執行下一行
一般新人很直接的想：加一個if的判斷碼，判斷每9個，才下一行。
但其實我們可以在第二個loop結束後，執行下一行的動作。

int main(){
    for(int y=1;y<=9;y++){
      for(int x=1;x<=9;x++){
         printf("%d * %d=%d",y,x,y*x );
         }
      printf("\n");
      }
return 0;
}

第二個loop執行結束時，便回到第一個loop作判斷，合乎條件再執行一次第二個loop
結果如下

======================分格======================

問題又出現了，下一句的輸出結果黏著上一句的輸出結果
這個時候\t(TAB) 用途要出現了

int main(){
    for(int y=1;y<=9;y++){
      for(int x=1;x<=9;x++){
         printf("%d * %d=%d\t",y,x,y*x );

         }
      printf("\n");
      }
return 0;
}

結果如下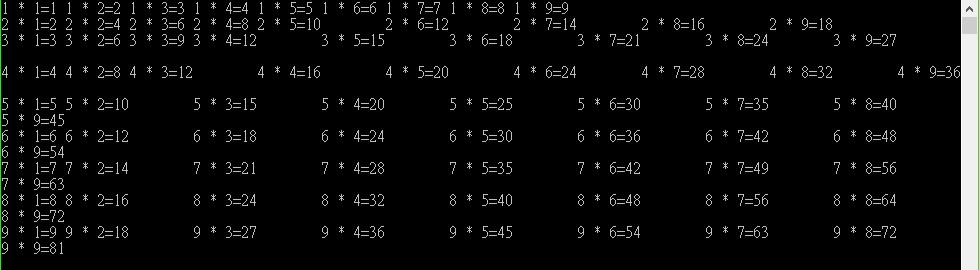

======================分格======================

噢不...句與句之間是有分格開，但怎麼變那麼醜?
老師說過：程式不會有錯，有錯的一定是人
我們仔細看一下，乘1的時候，排版都沒有偏差
但從乘2開始，程式所使用的\t，出現長短不一的距離
而且長TAB出現的位置都是前面是雙位數的結果；而短TAB出現的位置前面則是單位數的結果
首先，我會懷疑是不是\t前面輸出字元的長度，會影響\t所產生長短不一的間隔?
所以我把空白(Space)先刪去

#include <stdio.h>
#include <stdlib.h>
int main(){
    for(int y=1;y<=9;y++){
      for(int x=1;x<=9;x++){
         printf("%d*%d=%d\t",y,x,y*x );

         }
      printf("\n");
      }
return 0;
}

結果如下

======================分格======================
根據結果與理論，初步相信我的結論是對的
所以，我們來證明一下理論

int main(){
   printf("123456\t");
   printf("123456");
      printf("\n");
   printf("1234567\t");
   printf("1234567");
      printf("\n");
   printf("12345678\t");
   printf("12345678");
      printf("\n");
   printf("123456789\t");
   printf("12345678");
      printf("\n");
return 0;
}

結果如下

======================分格======================

在結果中，我們可以得知：當前一輸出字元長度超過7時，\t(TAB)會突然變超長
那我們知道\t前的輸出會影響\t(TAB)的長度，那\t後的輸出也會同樣影響到嗎？

int main(){
   printf("123456\t");
   printf("1234567891234");
      printf("\n");
   printf("1234567\t");
   printf("1");
      printf("\n");
   printf("12345678\t");
   printf("1");
      printf("\n");
   printf("123456789123456789\t");
   printf("1");
      printf("\n");
return 0;
}

結果如下

======================分格======================

結論：
根據輸出結果，我們看到\t的長度，只受前一輸出字元的長度而影響
\t是以每8個作一個區分，因為要留一空白作區隔，因此最高為7個字元
當超過7個字元時，電腦會自動幫你區分至下一個區段，因此會出現「突然變超長的情況」

解決辦法：
盡量統一輸出長度，方便\t排版
輸出長度盡可能為7+Nx8 (N為區隔數量)
為什麼是乘8，而不是乘7？
因為除了第一區隔不需要計算空白外，接下來的區隔，均要計算上一區隔所沒有佔用的空白。

======================分格======================

心得：
可能大家覺得只是\t排版遇到問題而且，修改一下，程式有美觀就可以了。
其實我當初寫九九乘法表，也是為了交作業，因此出現「結果出來就好了」的概念。
如果被老師問到「你根據什麼理論而寫這一行程式？」通常學生啞口無言，因為也不知道為什麼會出現這個結果。
因此希望從很簡單的程式入手，再參入一些研究方法，把大家常常忽略的東西，提出再加以驗證。

最後，其實我有點怕沒有主題可以寫，所以目前是分享撰寫程式的考慮及分析(當然，跟業界的工程師無法相比)，同時也為踏入研究所提早準備，一定要堅持30天。希望大家能給我鼓勵及評論(好壞也可以)
(其實我也沒有想到做九九乘法表，最後會思考\t排版問題...)