前言

最近上課老師讓我們用Scratch實作感知器，其實本身不太喜歡用這種，但其實跟寫程式的邏輯是差不多的，Scratch的繪製本身就是坐標系，可以省下換算位置的公式，很直觀的將程式實作並繪製。
在神經網路其實已經介紹過了，這次就讓我們使用它來做簡單分類並且了解原理和實作感知器。

主要流程

首先先回憶一下之前介紹的神經網路(NN)流程，這裡只多了前置步驟讓資料可視化。

1. 初始化點和其他資料
2. 繪製點和目前的分割線
3. 輸入點資料。
4. 乘上權重 + 偏權重(這裡當作多一個輸入)。
5. 活化函數(這裡使用sigmoid)。
6. 輸出函數(這裡無使用)。
7. 損失函數(這裡使用平均次方)。
8. 計算權重的反向傳播(偏微分)。
9. 更新(這裡使用SGD梯度下降)。
10. 回到第一步驟。

相關公式

這裡我選擇用神經網路提到的二元一次方程式來解說會比較明暸，在神經網路其實已經講過，這裡在更加詳細講解一次。

二元一次方程式

使用二元一次方程式ax + by + c = 0思考輸入乘上權重。

• 若c = 0，則ax + by會通過原點，所以a和b會影響到直線角度。
• 若a和b不變，則c = 1和c = 2差別為線的偏移位置不同。

由上述特性可知a和b控制角度，c控制偏移量。
二元一次方程式轉神經網路，將a和b與x和y轉為向量矩陣做內積w * x + b = 0。

正向傳播

1. w * x = y1
2. y1 + b = y

反向傳播(假設上層傳遞dout = [1, 1, 1] )
從正向步驟2反推回去計算變化(偏微分))。

1. db = dout * 1。加法的反向傳播直接傳遞
2. dy1 = dout * 1。加法的反向傳播直接傳遞
3. dw = dy1 * x。乘法反向傳播乘上x向量

帶入原公式：
db = 1。
dw = x。

最後使用梯度下降法(SGD)來去更新w -= lr * dw，b -= lr * db。

sigmoid函數。

這邊再複習一次sigmoid推導公式。
sigmoid公式：f(x)=1/(1 + e^(-x))。

正向傳播

1. -1 * x = y1。
2. e^y1 = y2。
3. 1 + y2 = y3。
4. 1 / y3 = y。

反向傳播(假設上層傳遞dout = [1])
方法一：從正向步驟4反推回去計算變化(偏微分))。

1. dy3 = dout * -1 / y3^2。導數的反向傳播1 / x = y，
2. dy2 = dy3 * 1。加法的反向傳播直接傳遞
3. dy1 = dy2 * y2。exp反向傳播不變
4. dx = dy1 * -1。乘法反向傳播乘上-1

帶入原公式：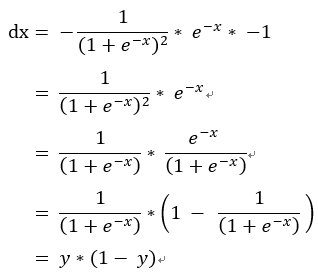

方法二：偏微分除法公式，帶入。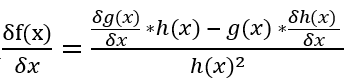

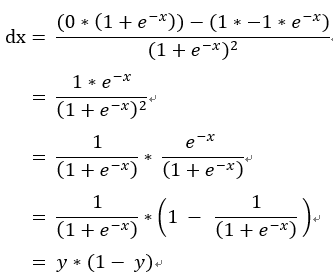
損失函數

均方誤差函數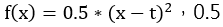：，0.5是為了偏微分所使用。

正向傳播

1. x – t = y1。
2. y1^2 = y2。
3. 0.5 * y2 = y。

反向傳播(上層傳遞dout = 1)
方法一：從正向步驟3反推回去計算變化(偏微分))。

1. dy2 = dout * 0.5。乘法反向傳播
2. dy1 = dy2 * y1。乘法反向傳播
3. dx = dy1 * 1。加法的反向傳播直接傳遞
4. dy1 = dy2 * y1。乘法反向傳播(計算第二個y1，因為裡面也有ｘ)
5. dx += dy1。加法的反向傳播直接傳遞(加上原先的dx)

帶入原公式：dx = x – t。

方法二：偏微分公式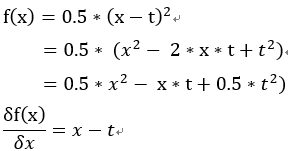

主要函數

• 建立畫線方塊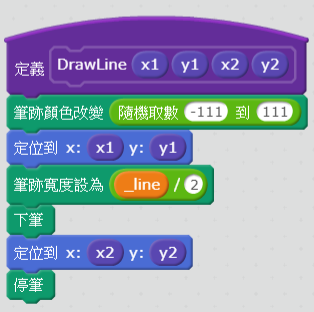
  

• 建立畫點方塊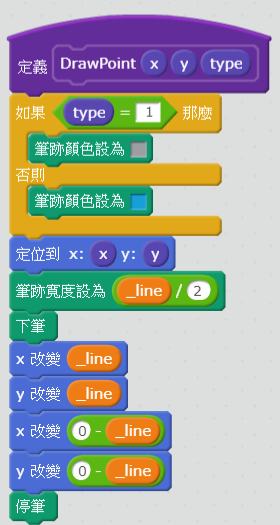
  

• 建立計算和畫出二元一次方塊
  

• 建立初始化資料方塊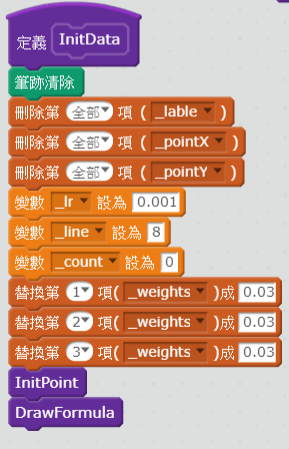
  

• 建立初始化隨機點方塊
  主要分兩類資料隨機取值，範圍如下x1∈[-180 ~ 180] ，
  y1∈[10 ~ 170] ，x2∈[-180 ~ 180]，y2 = [-10~-170]，並且設定標籤1和-1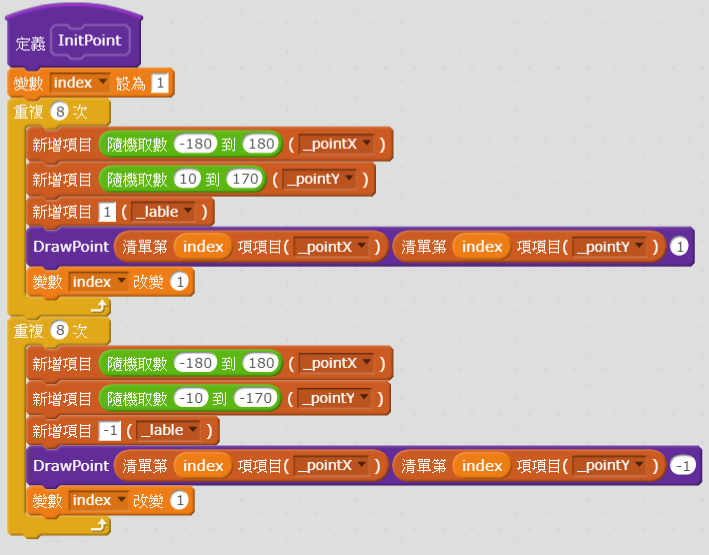
  

• 建立訓練方塊
  前向傳播這邊使用sigmod因為數據為[-1, 1]因此要走訪每個數據(無法先針對單一更新到loss = 0，階梯函數則可以)，loss大於0則計算反向傳播並且更新。
  

• 建立正向傳播方塊
  帶入正向傳播公式輸入 * 權重->活化函數(因這裡沒使用輸出函數所以這邊直接加總再用活化函數)->損失函數。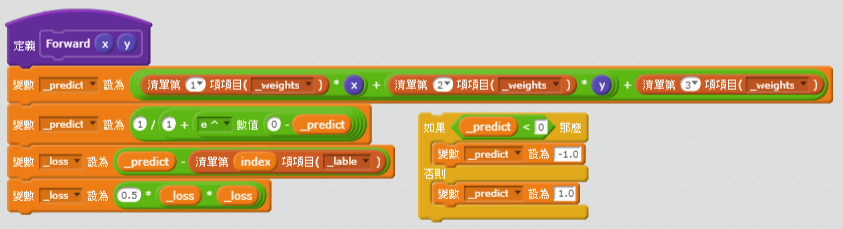
  

• 建立反向傳播方塊
  帶入反向傳播公式求”全部權重”的變化影響(偏微分)損失函數->活化函數。
  

• 建立更新增料方塊
  使用"全部權重"計算每個權重反向傳播並且更新。
  

結果

測試網址

結論

用起來其實算方便，但拉方塊的感覺還是不太喜歡，下次大概會教多層感知器或其他機器學習，有機會再跟大家分享。

參考文獻

[1]MNDTGhost.(2018) Perceptron感知器 from: https://scratch.mit.edu/projects/246182109/. (2018.10.04)
[2]MNGhost.(2018). [筆記]深度學習(Deep Learning)-神經網路學習 from: https://ithelp.ithome.com.tw/articles/10198796. (2018.10.04)