▌挑戰簡介

• 題目：計算機概論Ｘ30天

• 挑戰內容：連續30天紀錄計算機概論、離散數學、演算法、資料結構等課程，還有自己學習程式的心得體悟。

• 適合閱讀者
  • 認識時間複雜度
  • 看過我的上一篇Day5[演算法]如何衡量程式的效率？——論時間複雜度（Time Complexity）
• 不適合閱讀者
  • 不認識時間複雜度：請看上篇介紹Day5[演算法]如何衡量程式的效率？——論時間複雜度（Time Complexity）
  • 不會寫程式：初學者不需要會這個啦！
  • 太會寫程式：高手不需要看我胡說QQ

▌演算法（algorithm）的威力

前天說過如何利用算時間複雜度（Time Complexity）來檢測程式的效率，那今天就來介紹演算法（algorithm），但如果只是直接講解演算法定義，那肯定是很無聊，也不好懂。

尼采說「人們無法理解未曾經歷的事情」，還是直接看例子感受一下演算法的有趣吧！

1+2+3...+100怎麼算

要如何把1加到100呢？太簡單了，就用for迴圈囉！

function add() {
    var sum = 0;
    for (var i = 0; i <= 100; i++) {
        sum = sum + i  //0+1+2.....100停下來
    }
    console.log(sum)
}

go() //輸出5050

1+2+3...+n怎麼算

小看我的智商嗎？把100改成n放進去囉

function add(n) {
    var sum = 0;
    for (var i = 0; i <= n; i++) {
        sum = sum + i  //0+1+2.....n停下來
    }
    console.log(sum)
}

go(100) //輸出5050
go(200) //輸出20100

沒錯，這是解決問題的方法。

有更好的方法嗎？

高斯的演算法

數學小王子高斯說：「我有！」

聰明的數學家高斯，在小學的時候就想到了如何破解無聊老師給的「1加到100」這種莫名其妙的問題

當他的同學還在用1+2+3+...100慢慢算時，他直接用(1+100)X100%2解決了這個問題
也就是首項加末項乘以項數除以2

// 天才高斯的演算法，(1+100)*100/2

function gogo(n) {
    sum = (1 + n) * n / 2  
    console.log(sum)
}

gogo(100) //5050

所以呢？

哦....是喔...所以呢？

高斯的寫法是好在哪裡？

啊不就是比較短而已啊？

有什麼不一樣？

有！如果看過我的上一篇，就知道他們的時間複雜度（Time Complexity）不ㄧ樣！

時間複雜度（Time Complexity）分析

第一個寫法

function add(n) {
    var sum = 0;
    for (var i = 0; i <= n; i++) {
        sum = sum + i  //要跑n個迴圈，例如n=1000就要跑1000個迴圈
    }

}

第一個寫法因為使用了迴圈，當有n個數字時，就要跑n個迴圈，因此時間複雜度是O(n)

高斯寫法

function gogo(n) {
    sum = (1 + n) * n / 2  //不管n多大，例如n=1000000，這行也只用跑一次  
    console.log(sum) 
}

高斯的寫法不需要用到迴圈，不管n多大，也只需要一行，因此時間複雜度是O(1)

一個時間複雜度是O(n)，一個時間複雜度是O(1)

當n不大的時候兩者的執行效率不會差很多，但是當n愈來愈大時，高斯的演算法就會明顯地比他的同學還要好。

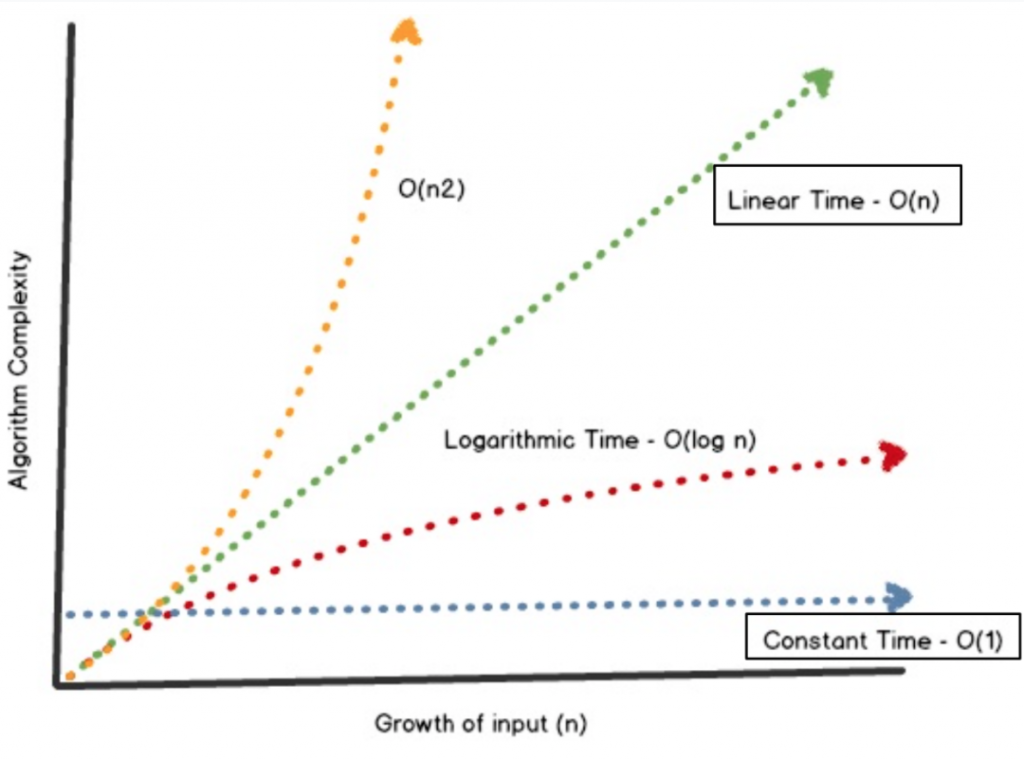
上圖呈現了當數據不同時，複雜度的差異

複習：時間複雜度不等同於「花費的時間」，而是指「隨著數據規模增大所增加的時間資源消耗變化」，因此又稱為漸進時間複雜度。

總結：什麼是演算法?

所以究竟什麼是算法(Algorithm)？
——說白了就是一套解決問題的方法（只不過把電腦的方法稱為「算法」感覺比較厲害）

那基於不同問題，計算機科學家就發明不同的方法

像是

• 處理數據排序問題：有氣泡排序（bubble sort)、插入排序（insertion sort）...等
• 處理資料搜索問題：有深度優先算法(DFS)、廣度優先算法(BFS)...等

不只是計算機，人做事也有方法，比如說「想閱讀書本第N章節的內容」，那「從目錄檢索」這個行為，可能就會比「從頭開始翻閱」來的有效率，更是一種好方法。

其實做事情的方法有很多，許多方法都能解決問題；只是一個「好方法」，更能比其他方法有效率解決問題。

就像高斯跟他同學的寫法，其實也都能解決問題。只是，在N很大的情況，高斯的演算法更明顯的有效率。

總而言之

如果說「方法」是人類解決問題的步驟，那「算法」就是電腦處理數據的步驟。
如果說「數據結構」是電腦儲存數據的的結構，「算法」就是電腦操作數據的一組方法。

算法這個詞聽起來很厲害，但其實不過就是一些處理問題的好步驟而已

參考資料與推薦閱讀

• 程杰，2011，《大話數據結構》：高斯的點子是從這裡來的
  這本書很有趣，整本以一個計算機教師為主角用對話的方式講解。
• 王爭・極客時間APP・《數據結構與算法之美》