指從某個頂點作為起點，依照某種順序，一個一個拜訪(visit)所有能到達的頂點。
走訪的順序分為: 廣度優先 (Breadth First Search) 和 深度優先 (Depth First Search)
由內而外，一層一層走訪的概念可以使用佇列結構。
以下圖為例子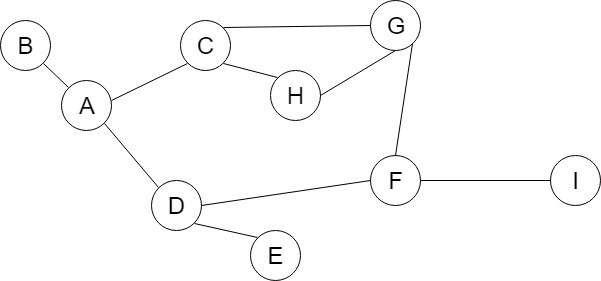
其中一組拜訪順序為
| A | [B，C，D] | [G，H，F，E] | [I] |
|---|---|---|---|
| 起點 | 第1層 | 第2層 | 第3層 |
| 動作說明 | Queue | 已走訪的頂點 |
|---|---|---|
| (0) 初始狀態 | (前) (尾) | 無頂點 |
| (1) 走訪頂點A，Enquene(A) | A | A |
| (2) Dequeue得到A，將與A相鄰且未被拜訪的頂點(B、C、D)逐一拜訪，並且Enqueue | B、C、D | A、B、C、D |
| (3) Dequeue得到B，B沒有與任何頂點相鄰 | C、D | A、B、C、D |
| (4) Dequeue得到C，C與G、H相鄰且未被拜訪，所以Enqueue (G)、(H) | D、G、H | A、B、C、D、G、H |
| (5) Dequeue得到D，D與E、F相鄰且未被拜訪，所以Enqueue (E)、(F) | G、H、E、F | A、B、C、D、E、G、H、E、F |
| (6) Dequeue得到G，G與C、H、F相鄰，但都被拜訪過了 | H、E、F | A、B、C、D、E、G、H、E、F |
| (7) Dequeue得到H，G與C、G、F相鄰，但都被拜訪過了 | E、F | A、B、C、D、E、G、H、E、F |
| (8) Dequeue得到E，E與D相鄰，但被拜訪過了 | F | A、B、C、D、E、G、H、E、F |
| (9) Dequeue得到F，F與G、I相鄰，但I沒被拜訪過，所以Enqueue (I) | I | A、B、C、D、E、G、H、E、F、I |
| (10) Dequeue得到I，I與F相鄰，但被拜訪過了 | 空 | A、B、C、D、E、G、H、E、F、I |
| (11) Queue 為空，停止 |
細談資料結構 第六版
ISBN 978-986-312-014-8
iThome鐵人賽
看影片追技術