前言

延續昨天的主題Spanning tree，昨天提到了DFS spanning tree跟BFS spanning tree。

今天要講的是Minimum (Cost) Spanning Tree。

Minimum (Cost) Spanning Tree

一個加權圖形G的任一個Spanning tree，其所有邊之加權總和，就是所謂的 Cost。
那麼，眾多Spanning tree中，所有邊的加權總和最小的，即為最少花費展開樹 Minimum Cost Spanning tree。

• 於Wikipedia的定義:

是一副** 連通加權無向圖** 中一棵權值最小的生成樹。

• 原圖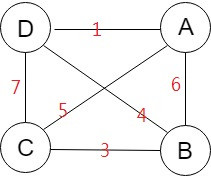
  

• Spanning tree T1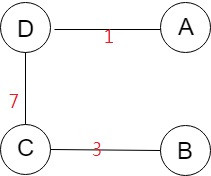
  

  • cost = 1 + 7 + 3 = 11

• Spanning tree T2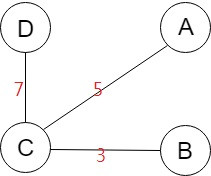
  

  • cost = 7 + 3 + 5 = 15

• Spanning tree T3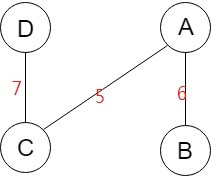
  

  • cost = 7 + 5 + 6 = 18

• 同一個圖形，不同cost的spanning tree。

想像

我們可以將原圖的四個頂點想像成我們要去的四個景點，其他六個邊是通往這4個景點的道路，其加權值就是需要花費的交通時間，任何一個Spanning tree都有將四個景點連通，如果我們挑選加權最少的spanning tree，也就是我們花費最少的交通時間就走訪完這四個景點。

=> 用最少的成本來達成目的，就是Minimum Spanning Tree的精隨!

Minimum Spanning Tree 要怎麼找呢?

能找到 Minimum Spanning Tree方法很多，著名的有Kruskal法、Prim法。
明天介紹找尋的方法吧。

參考

細談資料結構 第六版
ISBN 978-986-312-014-8

專有名詞還是用英文敘述會比較妥當。
像是Minimum Spanning Tree的中文有最少花費展開樹或是最小生成樹，又或是最小權重生成樹。
而且大多資訊領域的人在交流時，通常都是以英文來說專有名詞，反而說中文名詞有可能會讓人困惑。