前言

找Mininum spanning tree的方法有Kruskal's Algorithm和Prim's Algorithm，今天介紹Prim's Algorithm。

Prim's Algorithm

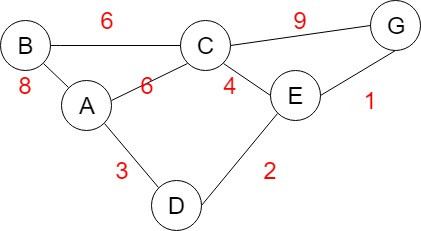
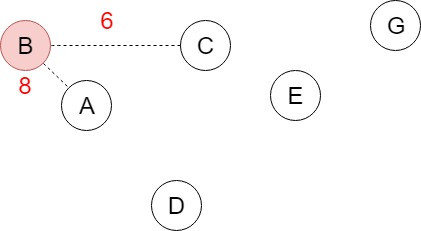
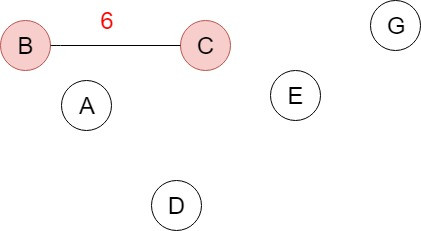
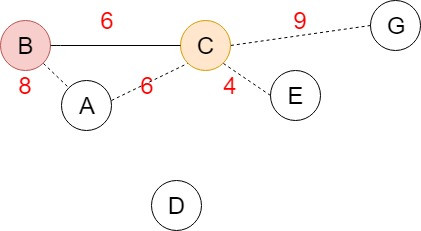
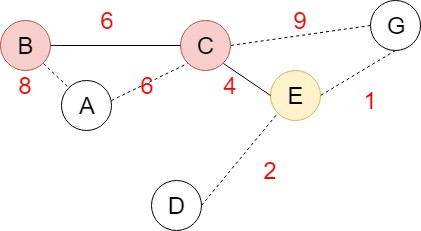
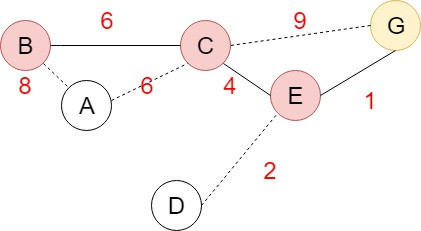
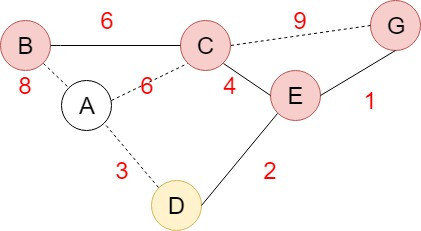
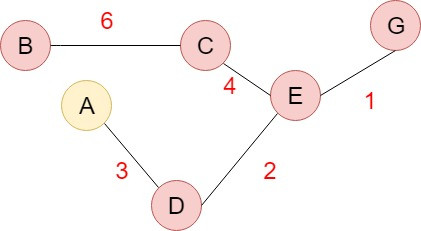
先從Spanning tree中找一個頂點V作為起始點，找出與V相連且還沒有被選取的頂點裡面加權值最小的邊，並加入與加權值最小的邊相連的頂點，重覆找尋相連且未被選取的頂點加入Spanning tree，直到產生了N-1個邊，將圖的N個頂點連接起來。

• 又到了以圖片為例子的時間了:
  
  1. 起始點設為B點，與B點相連的邊之權重值有6、8。
     
  2. 與B點相連的邊之最小權重值為6，且C點尚未被選取，於是加入頂點C。
     
  3. 又增加了C點的4個相鄰的邊，其權重值為4、6、8、9。
     
  4. 與B點或C點相連的邊之最小權重值為4，且E點尚未被選取，於是加入頂點E。
     
  5. 又增加了E點的2個相鄰的邊，其權重值為1、2。與B點或C點或E點相連的邊之最小權重值為3，且G點尚未被選取，於是加入頂點G。
     
  6. 與B點或C點或E點G點相連的邊之最小權重值為2，且D點尚未被選取，於是加入頂點D。
     
  7. 與B點或C點或E點G點D點相連的邊之最小權重值為3，且A點尚未被選取，於是加入頂點A。
     
     => 就找到Mininum spanning tree了~

參考

細談資料結構 第六版
ISBN 978-986-312-014-8