前言

Short Path 就是Graph中所有可能連通起點連到終點的path中，加權值最小的path。

昨天介紹的Dijkstra's Algorithm，只能計算Graph中從某一個起點到其餘各點的最短距離。
如果要求出任兩個頂點或是所有頂點間的最短距離，就必須使用 Floyd Algorithm。

Floyd-Warshall Algorithm

• 用途 : 找出有向圖所有兩點之間的最短路徑。

• 公式 :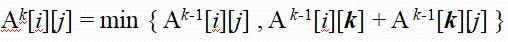

• 如果原本i點到j點的距離比經由k點的距離更遠，則採用經由k點的新距離，否則不變。

• 例子: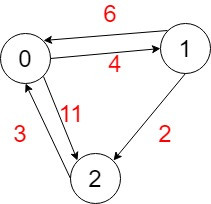
  

• A⁻¹為Adjacency matrix，表示i點到j點的最短距離，其間不經由任何節點。

• A°，經由頂點0的最短距離，其中2→1的距離已由∞更新成7

• A¹，經由頂點1的最短距離，其中0→2的距離已由11更新成6。

• A²，經由頂點2的最短距離，其中1→0的距離已由6更新成5。

=> 所有頂點間的最短路徑為A²所表示!

參考

細談資料結構 第六版
ISBN 978-986-312-014-8