閱讀前，建議可以參考Day1：閱讀指南＆為何選擇這個題目？

▌挑戰簡介

• 題目：計算機概論Ｘ30天

• 挑戰內容：連續30天紀錄計算機概論、離散數學、演算法、資料結構等課程，還有自己學習程式的心得體悟。

• 本篇性質：

  • 純粹上課內容的紀錄，不會有太嚴謹或是流暢的說明，因此不適合認真閱讀（怕你被誤導）
  • 如果真的要閱讀，最好要有bit、truth table、邏輯閘的基本知識，但我真的沒有時間寫的太清楚，因此看不懂請不要難過（可以看我心得就好）

▌前情提要

我從前就很奇怪，電腦裡面明明只有1010101（也就是ture/false），那所以是要怎麼做運算啊？我當然知道and/or/not這些電路的存在，可是說果我想要算102+320要怎麼辦？這跟邏輯差很多吧？

直到上了計算機概論，才知道如何把邏輯系統做加法系統

▌方法一：真值表

比如說，如果想要做2bit的加法要怎麼辦（像是01+00=01）

一個方法是畫truth table（真值表），然後用and/or/not寫出邏輯閘

Input=x1,x2,y1,y2（比如說01+01就是x1=0,x2=1,y1=0,y2=2)
output=z1,z2(比如說10，就是z1=1,z2=0)

and/or/not就可以處理true/false的問題

然後可以得得出：z1和z2分別是怎麼用and/or/not和x1,x2,y1,y2進行組合

但這種方法太爛了！！！！！只是2bit的加法我truth table（真值表）就寫了16行，如果是32bit加法就必須要寫2^64行......三小....誰有時間寫

因此用truth table的寫法是很麻煩的，2bit的寫法，無法用到4bit/8bit/64bit...的寫法上，因此是不可擴延的(not scalable)。

我們需要一個可擴延（scalable）的寫法

▌方法二：全加器

因此有個更好的方法，就是一次加1bit就好了，然後在串再一起

但要多一個carry in/out處理進位

Input=x,y,carry in
output=z,carry out

然後如果要n個bit的加法，就把n個全加器串再一起就好了

像是如果要8bit加法（像是10000000+11111111這種加法），就把8個全加器串在一起。

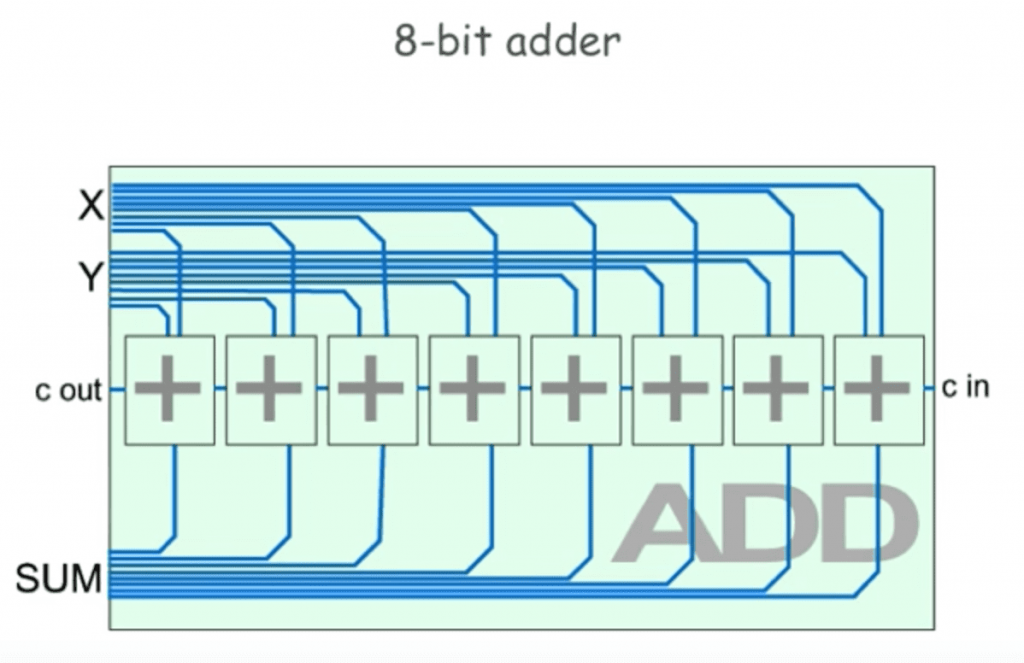
這樣的做法未必比用truth table做出的電路還要快，因為第二個全加器，需要等第一個全加器算完送出carry out後才能開始運算，但是他的好處就是不管是多少bit的加法器，都可以用這種方式去做

▌心得

• 世界上其實沒有一定好的好方法，以效率來說，truth table寫法得出的電路，可能是比較快的
• 但是以擴延性來說，全加器的寫法是更好用的（從1bit加法到100bit加法都可以用同一個模組串起來就好）