iT邦幫忙

2

[筆記]C++ & C#影像處理-機器學習AdaBoost訓練

c++ 機器學習
Kevin 2018-12-09 17:46:25 ‧ 3895 瀏覽

  • 分享至 

  • xImage
    •  

前言

偵測人臉或物體即將快到尾聲了，希望在12月底能完成相關的實作，也要給自己下一年新的目標，而我最困難的目標大概是英文/images/emoticon/emoticon04.gif。
這次要介紹機器學習的AdaBoost，AdaBoost原理其實很簡單，使用多個線性組合起來去分類，這裡最麻煩的地方應該是要推倒出分類器倍率的公式，但一步一步慢慢地去推導還是很容易理解的，接著就先介紹推倒公式。

推導公式

預測函數

每一次計算的加法模型。簡單來說就是每個線性判斷乘上倍率。
https://chart.googleapis.com/chart?cht=tx&chl=%24%24%20F(x)%20%3D%20%5Csum_%7Bm%3D0%7D%5EM%20%3D%20%5Calpha_mG_m(x)%20%24%24
Markdown

$$ F(x)=\sum_{m=0}^M=\alpha_mG_m(x) $$

損失函數

這裡使用指數損失函數。預測結果和實際相乘。
https://chart.googleapis.com/chart?cht=tx&chl=%24%24%20L(y%2CF(x))%3Dexp(-yf(x))%20%24%24

Markdown

$$ L(y,F(x))=exp(-yf(x)) $$

損失最小化函數(化簡和對alpha求偏微分=0)

目標為將指數損失最小化，將每一層的損失相加，而每個加法模型為上一層的結果加上目前計算的權重乘上分類結果G(x)，這樣做原因主要是將計算好的強分類器與目前的弱分類去做分離，方便後面計算alpha，將公式帶入。
https://chart.googleapis.com/chart?cht=tx&chl=%24%24%20(%5Calpha_m%2CG_m(x))%20%3D%20min%5Csum_%7Bi%3D1%7D%5EN%20exp(-y_i(f_%7Bm-1%7D(x_i)%20%2B%20%5Calpha%20G(x_i)))%20%24%24

Markdown

$$ (\alpha_m,G_m(x)) = min\sum_{i=1}^N exp(-y_i(f_{m-1}(x_i) + \alpha G(x_i))) $$

將上式拆解為兩部分，第一為前面已計算的強分類器函數，第二為目前要計算的弱分類器函數。

第一強分類器函數。
https://chart.googleapis.com/chart?cht=tx&chl=%24%24%20w_%7Bmi%7D%20%3D%20exp(-y_i%20f_%7Bm-1%7D(x_i))%20%24%24。

Markdown

$$ w_{mi} = exp(-y_i f_{m-1}(x_i)) $$

公式變為。
https://chart.googleapis.com/chart?cht=tx&chl=%24%24%20(%5Calpha_m%2CG_m(x))%20%3D%20min%5Csum_%7Bi%3D1%7D%5EN%20w_%7Bmi%7D%20exp(-y_i%20%5Calpha%20G(x_i))%20%24%24

Markdown

$$ (\alpha_m,G_m(x)) = min\sum_{i=1}^N w_{mi} exp(-y_i \alpha G(x_i)) $$

而第二個弱分類器函數要求的是alpha變化趨近0(偏微分)所以先化簡公式。G(x)函數主要是判斷分類分類正確或分類錯誤所以可將第二個函數拆開為分類正確函數加上分類錯誤，正確為1錯誤為-1帶入結果為。
https://chart.googleapis.com/chart?cht=tx&chl=%24%24%20g(%5Calpha)%20%3D%20exp(-%5Calpha_m)%5Csum_%7By%3DG_%7Bm(x_i)%7D%7D%5E%7B%7Dw_%7Bmi%7D%20%2B%20%20exp(%5Calpha_m)%5Csum_%7By%5Cneq%20G_%7Bm(x_i)%7D%7D%5E%7B%7Dw_%7Bmi%7D%20%24%24
Markdown

$$ g(\alpha) = exp(-\alpha_m)\sum_{y=G_{m(x_i)}}^{}w_{mi} +  exp(\alpha_m)\sum_{y\neq G_{m(x_i)}}^{}w_{mi} $$

接著化簡公式，多加了兩個合為0的sigma函數(2)，主要是能將其化簡為較簡單的函數(3)，最後將分類錯誤的函數轉為1~N的sigma函數(4)。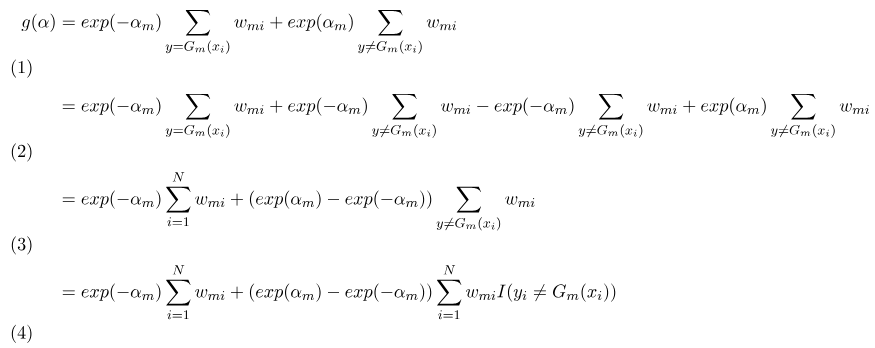
https://ithelp.ithome.com.tw/upload/images/20181205/20110564ZM3x4U2reo.png

Markdown

$$
\begin{align}
g(\alpha) &= exp(-\alpha_m)\sum_{y=G_m(x_i)}^{}w_{mi} + exp(\alpha_m)\sum_{y\neq G_m(x_i)}^{}w_{mi}\\
          &= exp(-\alpha_m)\sum_{y=G_m(x_i)}^{}w_{mi} + exp(-\alpha_m)\sum_{y\neq G_m(x_i)}^{}w_{mi} - exp(-\alpha_m)\sum_{y\neq G_m(x_i)}^{}w_{mi} + exp(\alpha_m)\sum_{y\neq G_m(x_i)}^{}w_{mi}\\
          &= exp(-\alpha_m)\sum_{i=1}^{N}w_{mi} + (exp(\alpha_m) - exp(-\alpha_m))\sum_{y\neq G_m(x_i)}^{}w_{mi}\\
          &= exp(-\alpha_m)\sum_{i=1}^{N}w_{mi} + (exp(\alpha_m) - exp(-\alpha_m))\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))
\end{align}
$$

對alpha求偏微分(變化) = 0，因為alpha都提出來且都在自然指數，所以依照公式其他地方可以忽略直接針對exp帶入偏微分(3)，最後偏微分結果為(4)。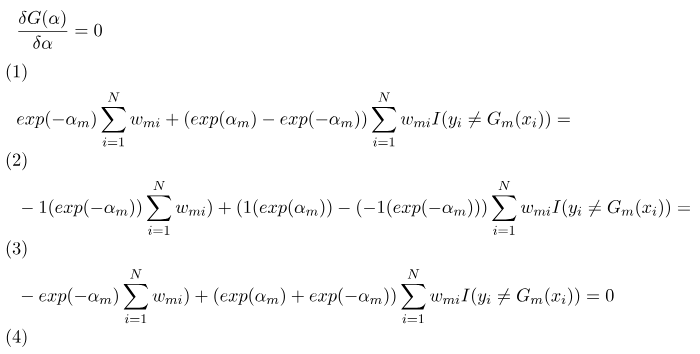
https://ithelp.ithome.com.tw/upload/images/20181205/20110564SflJr1w5Lg.png

Markdown

$$
\begin{align}
&\frac{\delta G(\alpha)}{\delta\alpha} = 0\\
&exp(-\alpha_m)\sum_{i=1}^{N}w_{mi} + (exp(\alpha_m) - exp(-\alpha_m))\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))=\\
&-1(exp(-\alpha_m))\sum_{i=1}^{N}w_{mi}) + (1(exp(\alpha_m))-(-1(exp(-\alpha_m)))\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))=\\
&-exp(-\alpha_m)\sum_{i=1}^{N}w_{mi}) + (exp(\alpha_m)+exp(-\alpha_m))\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i)) = 0
\end{align}
$$

接著求出alpha，以下為推導公式詳細過程。
https://ithelp.ithome.com.tw/upload/images/20181205/20110564Pff4Z71tDI.png

Markdown(em代替)

$$
\begin{align}
&-exp(-\alpha_m)\sum_{i=1}^{N}w_{mi} + (exp(\alpha_m)+exp(-\alpha_m))\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i)) = 0\\
&(exp(\alpha_m)+exp(-\alpha_m))\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i)) = exp(-\alpha_m)\sum_{i=1}^{N}w_{mi}\\
&(exp(\alpha_m)+exp(-\alpha_m))\frac{\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))}{\sum_{i=1}^{N}w_{mi}} = exp(-\alpha_m)\\
&\frac{(exp(\alpha_m)+exp(-\alpha_m))}{exp(-\alpha_m)}e_m = 1\\
&(exp(2\alpha_m)+1)e_m = 1
\\
&exp(2\alpha_m)e_m+e_m = 1\\
&exp(2\alpha_m)e_m = 1 - e_m\\
&exp(2\alpha_m) = \frac{1 - e_m}{e_m}\\
&2\alpha_m = ln(\frac{1 - e_m}{e_m})\\
&\alpha_m = \frac{1}{2}ln(\frac{1 - e_m}{e_m})
\end{align}
$$

Markdown(無代替)

$$
\begin{align}
&-exp(-\alpha_m)\sum_{i=1}^{N}w_{mi} + (exp(\alpha_m)+exp(-\alpha_m))\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i)) = 0\\
&(exp(\alpha_m)+exp(-\alpha_m))\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i)) = exp(-\alpha_m)\sum_{i=1}^{N}w_{mi}\\
&(exp(\alpha_m)+exp(-\alpha_m))\frac{\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))}{\sum_{i=1}^{N}w_{mi}} = exp(-\alpha_m)\\
&\frac{(exp(\alpha_m)+exp(-\alpha_m))}{exp(-\alpha_m)}\frac{\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))}{\sum_{i=1}^{N}w_{mi}} = 1\\
&(exp(2\alpha_m)+1)\frac{\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))}{\sum_{i=1}^{N}w_{mi}} = 1
\\
&exp(2\alpha_m)\frac{\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))}{\sum_{i=1}^{N}w_{mi}}+\frac{\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))}{\sum_{i=1}^{N}w_{mi}} = 1\\
&exp(2\alpha_m)\frac{\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))}{\sum_{i=1}^{N}w_{mi}} = 1 - \frac{\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))}{\sum_{i=1}^{N}w_{mi}}\\
&exp(2\alpha_m) = \frac{1 - \frac{\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))}{\sum_{i=1}^{N}w_{mi}}}{\frac{\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))}{\sum_{i=1}^{N}w_{mi}}}\\
&2\alpha_m = ln(\frac{1 - \frac{\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))}{\sum_{i=1}^{N}w_{mi}}}{\frac{\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))}{\sum_{i=1}^{N}w_{mi}}})\\
&\alpha_m = \frac{1}{2}ln(\frac{1 - \frac{\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))}{\sum_{i=1}^{N}w_{mi}}}{\frac{\sum_{i=1}^{N}w_{mi}I(y_i\neq G_m(x_i))}{\sum_{i=1}^{N}w_{mi}}})
\end{align}
$$

更新權重函數

而每個資料權重的公式，https://chart.googleapis.com/chart?cht=tx&chl=%24%24%20%5Csum_%7Bi%3D1%7D%5E%7BN%7Dw_%7Bmi%7D%20%24%24，會等於1，除了初始化和為一，還因為計算完後會將資料權重進行更新並且歸一化。
由上述分開的公式一我們得知上一個分類器權重公式為https://chart.googleapis.com/chart?cht=tx&chl=%24%24%20w_%7Bmi%7D%20%3D%20exp(-y_i%20f_%7Bm-1%7D(x_i))%20%24%24，而下一層就是將m+1，將公式拆開兩個式子(2)(上面有提到可將當下的權重拆開)，最後再變為最上面提到的加法模型(3)，以下推導簡化公式。

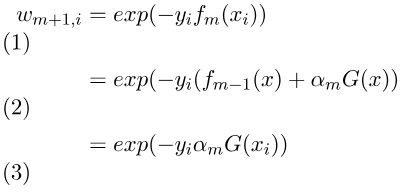
https://ithelp.ithome.com.tw/upload/images/20181205/20110564tsqZiFi8wc.png

Markdown

$$
\begin{align}
w_{m + 1,i} &= exp(-y_if_m(x_i))\\
&= exp(-y_i(f_{m-1}(x)+\alpha_mG(x))\\
&= exp(-y_i\alpha_mG(x_i))
\end{align}
$$

最後這裡使用L1歸一化，以下為公式。

https://chart.googleapis.com/chart?cht=tx&chl=%24%24%20%5Cbegin%7Balign%7D%20Z_m%20%26%3D%5Csum_%7Bi%3D1%7D%5ENexp(-y_i%5Calpha_mG(x_i))%20%5C%5C%20w_%7Bm%2B1%2Ci%7D%20%26%3D%20%5Cfrac%7Bw_%7Bm%2Ci%7D%7D%7BZ_m%7Dexp(-y_i%5Calpha_mG(x_i))%20%5Cend%7Balign%7D%20%24%24

Markdown

$$
\begin{align}
Z_m &=\sum_{i=1}^Nexp(-y_i\alpha_mG(x_i)) \\
w_{m+1,i} &= \frac{w_{m,i}}{Z_m}exp(-y_i\alpha_mG(x_i))
\end{align}
$$

AdaBoost實作

幾個月前剛碰AdaBoost找到程式碼後就沒仔細推導公式，這次參考[2]和[3]慢慢一步步的推導才理解，這裡實作主要用上述介紹的公式實作。

類別

我主要將公式實現拆開分為這三類，AdaBoost主要是訓練和預測，StrongClassfier和WeakClassfier則是儲存資料和強預測和弱預測。

  • AdaBoost：訓練資料和預測。
  • StrongClassfier：儲存弱分類器和預測強分類器。
  • WeakClassfier：弱分類器資料和預設弱分類器。

WeakClassfier類別

由上述推倒公式紀錄每一個弱分類器的資料，並且將每個分類器的權重alpha進行計算即可。而預測方面只需要使用維度索引與閥值依照分類比較符號進行比較即可。

資料成員

  • error:錯誤權重總和。
  • dimension:維度索引。
  • alpha:弱分類器權重。
  • sign:分類的比較符號。
  • threshold:分類闊值。

主要函數

  • Predict:無權重的預測結果(1　or　-1)。
  • WeightsPredict:有權重的預測結果(alpha　or　-alpha)。

程式碼

WeakClassfier.h

#pragma once
#ifndef WEAKCLASSIFIER_H
#define WEAKCLASSIFIER_H
#include "general.h"

/**********************************************************
 * pridect formula: alpha * compare(DATAS[dimension], threshold)
***********************************************************/
class WeakClassifier
{
public:
	enum SignType
	{
		BIG, SMALL
	};

	WeakClassifier();
	~WeakClassifier();

	WeakClassifier& operator=(const WeakClassifier& weakClassifier);

	AdaBoostType::LABELS Predict(AdaBoostType::C_DATAS& data, C_UINT32& dimension) const;

	std::vector<double> WeightsPredict(AdaBoostType::C_DATAS& data) const;

	double WeightsPredict(AdaBoostType::C_DATA& data) const;

	void Dimension(C_UINT32 dimension);
	UINT32 Dimension() const;

	void Threshold(C_DOUBLE threshold);
	double Threshold() const;

	double Alpha() const;

	void Error(C_DOUBLE sign);
	double Error() const;

	void Sign(const SignType sign);
	SignType Sign() const;

	void SetWeakParams(C_UINT32 dimension, C_DOUBLE threshold, C_DOUBLE alpha, const SignType sign);

	void SetWeakParams(C_UINT32 dimension, C_DOUBLE threshold, C_DOUBLE alpha);

private:
	typedef bool (*CMP_FM)(C_DOUBLE, C_DOUBLE);

	CMP_FM GetCompareFormula() const;

	UINT32 _dimension;
	double _threshold;
	double _alpha;
	double _error;
	SignType _sign;
};

#endif // !WEAKCLASSIFIER_H

WeakClassfier.cpp

#include "stdafx.h"
#include "WeakClassifier.h"

WeakClassifier::WeakClassifier()
{

}

WeakClassifier::~WeakClassifier()
{

}

WeakClassifier& WeakClassifier::operator=(const WeakClassifier& weakClassifier)
{
	_dimension = weakClassifier.Dimension();
	_threshold = weakClassifier.Threshold();
	_alpha = weakClassifier.Alpha();
	_sign = weakClassifier.Sign();

	return *this;
}

AdaBoostType::LABELS WeakClassifier::Predict(AdaBoostType::C_DATAS& data, C_UINT32& dimension) const
{
	C_UINT32 size = data.size();

	std::vector<__int32> predict(size);
	WeakClassifier::CMP_FM compare = GetCompareFormula();

	for (UINT32 index = 0; index < size; index++)
	{
		if (compare(data[index][dimension], _threshold))
		{
			predict[index] = 1;
		}
		else
		{
			predict[index] = -1;
		}
	}
	return predict;
}

std::vector<double> WeakClassifier::WeightsPredict(AdaBoostType::C_DATAS& data) const
{
	C_UINT32 size = data.size();

	std::vector<double> predict(size);
	WeakClassifier::CMP_FM compare = GetCompareFormula();

	for (UINT32 index = 0; index < size; index++)
	{
		if (compare(data[index][_dimension], _threshold))
		{
			predict[index] =  _alpha;
		}
		else
		{
			predict[index]= -_alpha;
		}
	}
	return predict;
}

double WeakClassifier::WeightsPredict(AdaBoostType::C_DATA& data) const
{
	WeakClassifier::CMP_FM compare = GetCompareFormula();

	if (compare(data[_dimension], _threshold))
	{
		return _alpha;
	}
	else
	{
		return -_alpha;
	}
}

WeakClassifier::CMP_FM WeakClassifier::GetCompareFormula() const
{
	switch (_sign)
	{
	case SignType::SMALL:
		return [](C_DOUBLE value, C_DOUBLE threshold) {return value <= threshold; };
	case SignType::BIG:
		return [](C_DOUBLE value, C_DOUBLE threshold) {return value > threshold; };
	default:
		return [](C_DOUBLE value, C_DOUBLE threshold) {return value <= threshold; };
	}
}

void WeakClassifier::Dimension(C_UINT32 dimension)
{
	_dimension = dimension;
}

UINT32 WeakClassifier::Dimension() const
{
	return _dimension;
}

void  WeakClassifier::Threshold(C_DOUBLE threshold)
{
	_threshold = threshold;
}

double  WeakClassifier::Threshold() const
{
	return _threshold;
}

void WeakClassifier::Error(C_DOUBLE error)
{
	_error = error;
	_alpha = 0.5 * log((1.0 - error) / std::max(error, 0.0000000000001)) / log(exp(1));
}

double WeakClassifier::Error() const
{
	return _error;
}

double WeakClassifier::Alpha() const
{
	return _alpha;
}

void WeakClassifier::Sign(const SignType sign)
{
	_sign = sign;
}

WeakClassifier::SignType WeakClassifier::Sign() const
{
	return _sign;
}

void WeakClassifier::SetWeakParams(C_UINT32 dimension, C_DOUBLE threshold, C_DOUBLE error, const SignType sign)
{
	Dimension(dimension);
	Threshold(threshold);
	Error(error);
	Sign(sign);
}

void WeakClassifier::SetWeakParams(C_UINT32 dimension, C_DOUBLE threshold, C_DOUBLE error)
{
	Dimension(dimension);
	Threshold(threshold);
	Error(error);
}

StrongClassfier類別

強分類器主要儲存弱分類器與弱分類器的加總和預測結果。也就是最一開始介紹的加法模型公式。

資料成員

  • weakClassifiers:所有的弱分類器。

主要函數

  • Predict:預測結果(1　or　-1)。

程式碼

StrongClassfier.h

#pragma once
#ifndef STRONGCLASSFIER_H
#define STRONGCLASSFIER_H
#include "general.h"
#include "WeakClassifier.h"

/**********************************************************
* pridect formula: sign(sum(weakClassfier.weightsPredict()))
***********************************************************/
class StrongClassfier
{
public:
	StrongClassfier();
	~StrongClassfier();

	void Add(const WeakClassifier& weakClassifier);

	AdaBoostType::LABELS Predict(AdaBoostType::C_DATAS& data) const;

	AdaBoostType::LABEL Predict(AdaBoostType::C_DATA& data) const;

	AdaBoostType::LABELS Sign(const std::vector<double>& predict) const;

	AdaBoostType::LABEL Sign(const double predict) const;

private:
	std::vector<WeakClassifier>* _weakClassifiers;

};

#endif

StrongClassfier.cpp

#include "stdafx.h"
#include "StrongClassfier.h"

StrongClassfier::StrongClassfier()
{
	_weakClassifiers = new std::vector<WeakClassifier>();
}

StrongClassfier::~StrongClassfier()
{
	delete _weakClassifiers;
	_weakClassifiers = nullptr;
}

void StrongClassfier::Add(const WeakClassifier& weakClassifier)
{
	_weakClassifiers->push_back(weakClassifier);
}

AdaBoostType::LABELS StrongClassfier::Predict(AdaBoostType::C_DATAS& data) const
{
	AdaBoostType::LABELS predict(data.size());

	for (UINT32 index = 0; index < data.size(); index++)
	{
		predict[index] = Predict(data[index]);
	}

	return predict;
}

AdaBoostType::LABEL StrongClassfier::Predict(AdaBoostType::C_DATA& data) const
{
	double predict = 0;
	for (UINT32 index = 0; index < _weakClassifiers->size(); index++)
	{
		const double weakPredict = _weakClassifiers->at(index).WeightsPredict(data);

		for (UINT32 predIndex = 0; predIndex < data.size(); predIndex++)
		{
			predict += weakPredict;
		}
	}
	return Sign(predict);
}


AdaBoostType::LABELS StrongClassfier::Sign(const std::vector<double>& predict) const
{
	AdaBoostType::LABELS labels(predict.size());

	for (UINT32 index = 0; index < predict.size(); index++)
	{
		labels[index] = Sign(predict[index]);
	}
	return labels;
}

AdaBoostType::LABEL StrongClassfier::Sign(const double predict) const
{
	return predict > 0 ? 1 : -1;
}

AdaBoost類別

構想

1.輸入N筆訓練資料和N筆標籤。
2.預設資料的分類權重=1/N筆。
3.訓練並給予訓練次數T。
4.找出目前分類權重錯誤率最小的閥值，並更新弱分類器。
5.更新分類權重，重複直到次數T。
6.輸入資料，預測結果。

資料成員

  • data:訓練資料。
  • label:標籤。
  • strongClassfier:強分類器。
  • dataWeights:訓練資料目前權重。
  • dimensionSize:維度大小。
  • dataSize:資料數量。

主要函數

  • Predict:預測結果。
  • Train:訓練資料。
  • ProcessError:找尋當下目前錯誤率最小的弱分類器。走訪每個資料、維度和比較符號並使用弱分類器預測結果。
  • CalcError:計算弱分類器預測與實際標籤的錯誤權重。
  • UpdateWeights:更新權重。依照找尋到錯誤率最小的弱分類器和結果依照公式更新下一輪的權重。

程式碼

AdaBoost.h

#pragma once
#ifndef ADABOOST_H
#define ADABOOST_H
#include "general.h"
#include "StrongClassfier.h"
#include "WeakClassifier.h"

class AdaBoost
{

public:
	AdaBoost(AdaBoostType::C_DATAS& data, AdaBoostType::C_LABELS label) :_data(data), _label(label){ Init(); };
	~AdaBoost();

	void Train(C_UINT32 weakSize);
	AdaBoostType::LABELS Predict(AdaBoostType::C_DATAS& data) const;
	AdaBoostType::LABEL Predict(AdaBoostType::C_DATA& data) const;
private:
	void Init();
	void ProcessError(WeakClassifier& weakClassifier, AdaBoostType::LABELS& pridect);
	double CalcError(AdaBoostType::C_LABELS& pridect);
	void UpdateWeights(const WeakClassifier& weakClassifier, AdaBoostType::C_LABELS& pridect);

	AdaBoostType::C_DATAS _data;
	AdaBoostType::C_LABELS _label;

	StrongClassfier* _strongClassfier;
	std::vector<double>* _dataWeights;
	UINT32 _dimensionSize;
	UINT32 _dataSize;

};

#endif // !ADABOOST_H

AdaBoost.cpp

#include "stdafx.h"
#include "AdaBoost.h"

AdaBoost::~AdaBoost()
{
	delete _dataWeights;
	_dataWeights = nullptr;

	delete _strongClassfier;
	_strongClassfier = nullptr;
}

void AdaBoost::Init()
{
	assert(_data.size() > 0 && _data[0].size() > 0);

	_dataSize = _data.size();
	_dimensionSize = _data[0].size();
	_dataWeights = new std::vector<double>(_dataSize, 1.0 / _dataSize);
	_strongClassfier = new StrongClassfier();
}


void AdaBoost::Train(C_UINT32 weakSize)
{
	for (UINT32 index = 0; index < weakSize; index++)
	{
		WeakClassifier weakClassifier;
		AdaBoostType::LABELS pridect;

		ProcessError(weakClassifier, pridect);

		UpdateWeights(weakClassifier, pridect);

		_strongClassfier->Add(weakClassifier);
	}
}

void AdaBoost::ProcessError(WeakClassifier& minWeakClassifier, AdaBoostType::LABELS& minPridect)
{
	WeakClassifier weakClassifier;

	double minError = 100000;

	for (UINT32 dimension = 0; dimension < _dimensionSize; dimension++)
	{
		weakClassifier.Dimension(dimension);

		for (UINT32 index = 0; index < _dataSize; index++)
		{
			weakClassifier.Threshold(_data[index][dimension]);

			const WeakClassifier::SignType signs[] = { WeakClassifier::SignType::BIG
				, WeakClassifier::SignType::SMALL };

			for (UINT32 signIndex = 0; signIndex < sizeof(signs) / sizeof(WeakClassifier::SignType); signIndex++)
			{
				weakClassifier.Sign(signs[signIndex]);

				const std::vector<__int32> pridect = weakClassifier.Predict(_data, dimension);
				C_DOUBLE error = CalcError(pridect);

				if (error < minError)
				{
					minWeakClassifier = weakClassifier;
					minPridect = pridect;
					minError = error;
				}
			}

		}
	}
	minWeakClassifier.Error(minError);
}

double AdaBoost::CalcError(AdaBoostType::C_LABELS& pridect)
{
	assert(pridect.size() == _label.size());

	double error = 0.0;

	for (UINT32 index = 0; index < _dataSize; index++)
	{
		if (pridect[index] != _label[index])
		{
			error += _dataWeights->at(index);
		}
	}

	return error;
}

void AdaBoost::UpdateWeights(const WeakClassifier& weakClassifier, AdaBoostType::C_LABELS& pridect)
{
	double sum = 0;

	for (UINT32 index = 0; index < _dataSize; index++)
	{
		_dataWeights->at(index) *= exp(-weakClassifier.Alpha() * pridect[index] * _label[index]);
		sum += _dataWeights->at(index);
	}

	for (UINT32 index = 0; index < _dataSize; index++)
	{
		_dataWeights->at(index) /= sum;
	}

}

AdaBoostType::LABELS AdaBoost::Predict(AdaBoostType::C_DATAS& data) const
{
	return _strongClassfier->Predict(data);
}

AdaBoostType::LABEL AdaBoost::Predict(AdaBoostType::C_DATA& data) const
{
	return _strongClassfier->Predict(data);
}

結果

使用[4]的資料測試結果，比對後誤差不大。

// AdaBoostAPI.cpp : Defines the entry point for the console application.
//

#include "stdafx.h"
#include "AdaBoost.h"
#include "general.h"
#include <iostream>
int main()
{
	AdaBoostType::DATAS data = { {0}, {1},{ 2 },{ 3 },{ 4 },{ 5 },{ 6 },{ 7 },{ 8 },{ 9 } };

	AdaBoostType::LABELS label = { 1, 1, 1, -1, -1, -1, 1, 1, 1, -1 };

	AdaBoost adaBoost(data, label);
	adaBoost.Train(5);

	AdaBoostType::LABELS labels = adaBoost.Predict(data);
	for (UINT32 index = 0; index < labels.size(); index++)
	{
		std::cout << labels[index] << " ";
	}

	system("pause");
	return 0;
}

AdaBoostAPI

結語

這禮拜跳過"Selective Search for Object Recognition"主要原因是想把論文看完，所以這禮拜先介紹AdaBoost，若有問題或錯誤歡迎提問。

參考文獻

[1]https://upmath.me/
[2]liuwu265@126.com(2015) AdaBoost 算法原理及推导 https://www.cnblogs.com/liuwu265/p/4692347.html(2018.12.05)
[3]SIGAI(2018). 理解AdaBoost算法 form:https://zhuanlan.zhihu.com/p/43443518(2018.12.05)
[4]v_JULY_v(2014) Adaboost 算法的原理与推导 form:https://blog.csdn.net/v_JULY_v/article/details/40718799(2018.12.08)


圖片
  直播研討會
圖片
{{ item.channelVendor }} {{ item.webinarstarted }} |
{{ formatDate(item.duration) }}
直播中

尚未有邦友留言

立即登入留言
iThome鐵人賽
參賽組數
1064 組
團體組數
40 組
累計文章數
22207 篇
完賽人數
600 人
iT+看影片追技術 看影片追技術 看更多
熱門tag 看更多
15th鐵人賽 16th鐵人賽 13th鐵人賽 14th鐵人賽 12th鐵人賽 11th鐵人賽 鐵人賽 2019鐵人賽 javascript 2018鐵人賽 python 2017鐵人賽 windows php c# windows server linux css react vue.js
熱門問題
熱門回答
熱門文章
IT邦幫忙