密碼學(Cryptography)一詞的英文來自兩個古希臘詞彙kryptós(隱藏的)和gráphein(書寫),因此古典密碼學主要著重在資訊傳遞與保密,隨著資訊的進步也衍伸出各種不同的加密形式以確保資料傳遞時的安全,比方說Https與SSL等,都是密碼學在網路技術上的應用以確保我們平時上網的資訊與足跡不至於洩漏。
在討論密碼學之前我們先從四個最基本的名詞介紹起,分別是:
區塊鏈使用到大量加密的技術,因此前面三個(編碼、壓縮、哈希)我們只會簡單提到它們的功能與應用,到了加密才會研究演算法是如何被實作出來的。今天我們先介紹其中兩個:編碼與壓縮
對於電腦而言是只有0與1的存在,每個0或1就是一個bit(位元),8個0或1組合起來便是一個bytes(位元組),除了0與1外其他一概不認。但這樣會造成使用上非常地不便,於是我們就把0與1加以編碼,規定了每一組0跟1分別代表的字元,最有名的編碼表莫過於Ascii碼表,Ascii碼表的編碼單位是位元組,每個獨立的位元組都可以透過Ascii碼表轉換成一種字元,在古早的時代拿來做資訊交換或排版的工具。
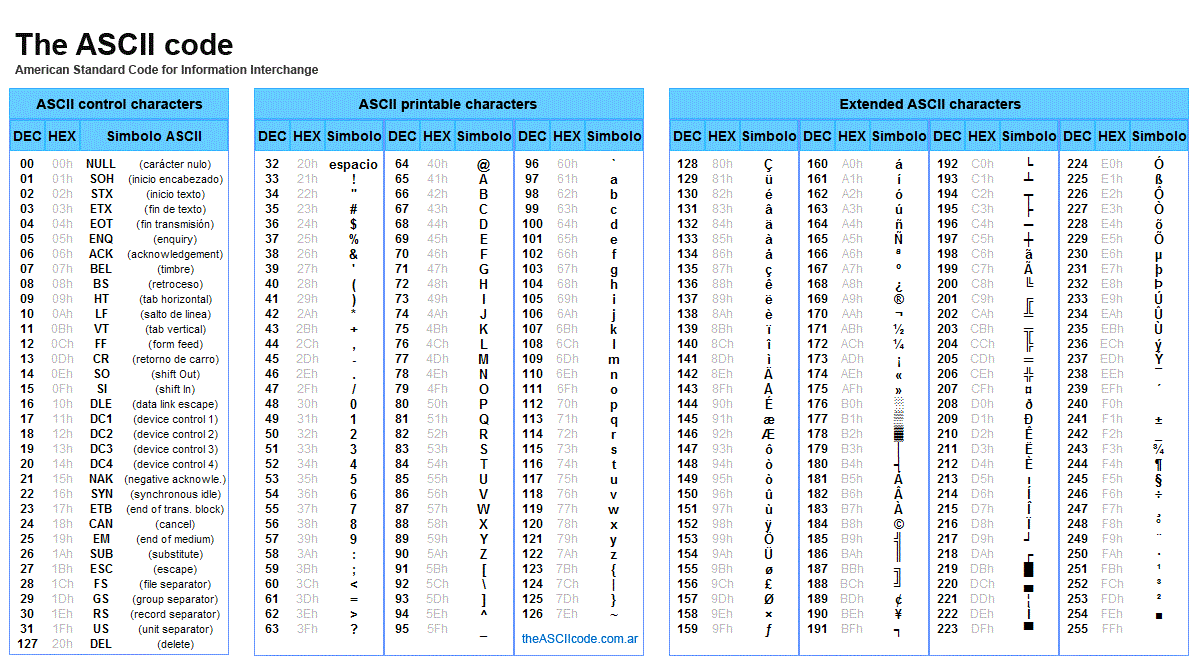
圖片來源:commons wikimedia
比方說我們要跟對方說Hi,透過這張表,我們會把大寫H轉換成72、小寫i轉換成105,同時這兩個的位元組分別是01001000(H)、01101001(i),實際上我們電腦傳給對方電腦的是01001000、01101001這兩個位元組。
所以編碼又可以看做是資料間的轉換。而且因為編碼通常兩邊、甚至第三方都有同一張表格,彼此也都知道轉換方式,編碼的目的往往是希望資料能夠被順利傳遞與解讀,為了傳遞效率的考量,通常編碼的研究著重在如何編碼所耗去的資料空間較小與避免轉碼出錯上。
如果傳遞資訊方編碼(Encode)與接收資訊方解碼(decode)使用的表格不同,就會造成亂碼的情形。
過去瀏覽外國網站時常常有亂碼的出現,UTF-8的出現解決了這個問題,它把世界上所有語言與各種奇形怪狀的符號通通編碼進去,也因為編入的字體多很多,因此UTF-8使用的空間較大(一至四個位元組)為每個字元編碼(相較於Ascii碼表只需要一個Bytes就可以完成)。
而有些中文字的編碼是使用Big5編碼,讓每個中文字使用2bytes。
除了文字的轉換外,常見的jpg、mp4等圖片影音轉檔等也都是常見編碼的應用,透過把資料編碼達到資訊傳遞的效果。
壓縮的目的是將原始的檔案資料經過數學演算法重新計算、編排或編碼後,達到所需儲存空間減少的功能,最知名的壓縮軟體莫過於大家都用過但從不付錢的WINRAR,就像斯斯有兩種一樣,壓縮演算法也可以大概分類成兩種:失真壓縮與無失真壓縮。
無失真壓縮代表資料及便經過壓縮後,也可以解壓縮回跟原本完全一模一樣的資料。通常適用在文字或數據的傳地上,畢竟這樣的資料是不允許任何小瑕疵或更動的,但也因為必須保持資料的一致性,壓縮率通常會比較低,所以如果壓縮一份普通的純文字檔,通常會發現壓縮率不甚理想。
下面這張圖展示的是圖片的無失真壓縮,左上角的Bitmap表示的是原始資料未經過壓縮,共需要696KB,經過JPEG壓縮之後僅僅需要43.3KB的空間儲存,這也是為什麼通常我們下載下來的檔案格式通常是jpeg了!(資料來源)

失真壓縮指的是資料經過壓縮後無法解壓縮回原本的資料,會有部分的失真或偏移,通常應用在影像或是聲音的壓縮上,因為這類的資料極便產生了微小的偏移,對大部分人的觀賞還是不會產生很大的影響(專業的玩家使用的就是無失真壓縮了)。失真壓縮的好處是可以根據需要的品質與空間大小輸出成相對應大小的檔案,這在網頁的瀏覽體驗非常重要,網頁的資源通常80%以上都是圖片,原始碼是文字格式所以占用的空間不大,因此圖片的壓縮對於網頁的瀏覽速度非常重要。
下面展示的是圖片的失真壓縮,可以看到隨著需求品質的下降,所需的儲存大小也跟著下降。(資料來源)
至於怎麼做到壓縮的呢?以最知名、最入門的壓縮演算法─霍夫曼(Hoffman)編碼為例,想法概念就是把最常見、出現頻率最高的資料用最小的空間去轉存或重新編碼。
舉例來說我們現在有段文字需要壓縮,這段文字如下
ABCADBDDDADBDA
如果我們任意編碼成下面格式
A:00、B、01、C:10、D:11
那麼我們總共需要28 bits的儲存空間,你可能會有一個疑問為什麼不能用一個位元去編碼呢?像是:
A:0、B、1、C:00、D:01
因為這樣的話如果你收到01,那麼根本不知道要解成A(0)B(1)、或是D(01)!所以我們在編碼的過程也必須考慮是否能順利解碼,以剛剛的編碼格式為例,因為每兩個位元都是一組編碼,所以我們可以兩兩一組很順利的把編碼解出來。
那霍夫曼編碼是怎麼做的呢?首先我們先計算每個文字出現的頻率:A→4次、B→3次、C→1次、D→6次,因為D產生最多次、我們透過二元樹編給它

D:0、A:10、C:110、B、111
於是原本的資料就可以壓縮成
10111110100111000100111010
壓縮後的資料僅需要26 bits便可以儲存!至於詳細的實作可以參考這裡。
解碼的過程也是透過二元樹去解碼,從最開頭去解碼,直到解出最底層的頁節點為止,也因此在我們這個例子的編碼中並沒有編入1、01、00、01這幾種編碼,這是為了解碼時能夠順利被解碼出唯一一組解。
你也可以發現霍夫曼是透過改善編碼的方式來達到壓縮資料的目的,採取的作法是一個個字詞單一去處理,直到後來已經慢慢被算術編碼所取代,算術編碼是直接把整個輸入的訊息編碼為一個數,有興趣實做的話可以參考這裡。
到目前為止的文章都會放置在Github上。
