我們前天提到了下面四個名詞,並且已經解釋完編碼、壓縮、哈希:
因此今天我們最後要介紹:加密

加密(Encrypt)的目的是我們想要讓只有特定第三方能夠讀取我們的訊息,以上面這個圖為例,我們在發送訊息前將我們的原始訊息(明文,Plaintext)加密(Encrypt)成Kl,那麼即便傳遞訊息的過程中信使被攔截,攔截者看到的也只是一段加密過後的文字(密文,Cipertext),從而確保了資訊的安全。如果我們想要取得原始的資料,那麼也只需要透過金鑰(Key)去解密便可以了!
網路時代的資訊安全是奠基在密碼學之上的,我們每天在網路上傳遞各式各樣的訊息,私人傳遞的訊息自然不希望被第三者瀏覽、登入的密碼更是萬萬不可被中間人截取到、操作網路atm進行提匯款的時候更要再三確認使用者的身分,因此如何避免資訊被截取、破譯與偽造是現今網路時代的一大課題,我們首先來看加密法的大原則 :
Auguste Kerckhoffs在19世紀提出的幾個加密系統需要有的原則:
加密方法被洩漏後仍應保持安全性,在任何的狀態下,都必須假定加密方法已經被敵人取得,否則一旦日後發現已經被敵人知悉,更換任何金鑰都是徒勞。不只有Auguste Kerckhoffs提倡這件事,著名的密碼學學者Claude Shannon與Bruce Schneie也都有類似的想法。
"The enemy knows the system" - Claude Shannon
"Security through obscurity." - Bruce Schneie
在進入現代的加密法之前,我們來看看幾種古典的加密法,雖說目前這幾種加密法都可以輕易地被電腦破譯,但其實大部分的現代加密法背後的精神跟原理都是源自於古典加密法。

圖片來源:Basics of Cryptography: Caesar Cipher
Caesar加密據傳聞是歷史課本上的那個凱薩所發明的,它的方法簡單而暴力,就是把每個字母偏移幾個作為替換,比方說往右偏移三個,也就是A都改成D、B都改成E、C都改成F....作為替代文字,簡單而硬漢(?)的方式讓它可以很快地被加解密,但缺點也很明顯:英文字母不就那26個,要暴力解出來也只需要嘗試25次就可以解出來了。我們最開頭把Hi轉換成Kl其實也是Caesar加密法!
下面是Caesar加密的簡單python實作,先取得字母的次序後,再平移,這裡我們定義加密是把ascii碼增加、解密則是把ascii碼減少:
def txt_shift(txt, shift):
result = ""
for idx in range(0, len(txt)):
char = txt[idx]
if char.isalpha():
if char.isupper():
order = ord(char) -65 + shift
order %= 26
order += 65
elif char.islower():
order = ord(char) -97 + shift
order %= 26
order += 97
char = chr(order)
result += char
return result
def caesar_encryption(txt, shift):
return txt_shift(txt, shift)
def caesar_decryption(txt, shift):
return txt_shift(txt, -1 * shift)
plain_txt = "Hello!"
shift_amount = 10
print(f"原始明文: {plain_txt}")
cipher_txt = caesar_encryption(plain_txt, shift_amount)
print(f"加密密文: {cipher_txt}")
decryption_cipher_txt = caesar_decryption(cipher_txt, shift_amount)
print(f"解密結果: {decryption_cipher_txt}")
就可以得到加解密的結果如下:
原始明文: Hello!
加密密文: Rovvy!
解密結果: Hello!
但Caesar加密法被洩漏後即便不知道偏移個數,但只要嘗試25次就可以破譯,很明顯的Caesar加密不符合Kerckhoffs's principle。

Caesar加密實在太容易被破解了,簡單改進Caesar加密的方法就是不要固定偏移幾個字元,而是另外開一張表做隨機的對應,比方說我們開一個新的對應表格:A→F、B→T、C→J代替,我們的表格總共會有26!總可能。
下面是Monoalphabetic加密的簡單實作,先透過隨機數取得字母的代換表後,加密時再根據代換表把原始明文的字母替換掉,解密的時候則需要把該代換表反轉過來:
from random import sample
def txt_shift(txt, shift):
result = ""
for idx in range(0, len(txt)):
char = txt[idx]
if char.isalpha():
order = ord(char)
if char.isupper():
order -= 65
order = shift[order]
order += 65
elif char.islower():
order -= 97
order = shift[order]
order += 97
char = chr(order)
result += char
return result
def mono_encryption(txt, shift):
return txt_shift(txt, shift)
def mono_decryption(txt, shift):
inverse_shift = [0] * 26
for idx, value in enumerate(shift):
inverse_shift[value] = idx
return txt_shift(txt, inverse_shift)
plain_txt = "Hello!"
shift_list = sample(range(0,26), 26)
print(f"原始明文: {plain_txt}")
print(f"Monoalphabet: {shift_list}")
cipher_txt = mono_encryption(plain_txt, shift_list)
print(f"加密密文: {cipher_txt}")
decryption_cipher_txt = mono_decryption(cipher_txt, shift_list)
print(f"解密結果: {decryption_cipher_txt}")
就可以得到以下的執行結果:
原始明文: Hello!
Monoalphabet: [23, 8, 24, 0, 1, 4, 5, 22, 10, 12, 19, 7, 6, 20, 3, 14, 2, 21, 15, 17, 9, 16, 13, 18, 11, 25]
加密密文: Wbhhd!
解密結果: Hello!
看起來似乎萬無一失了,但實際上不是的。
事情不會那麼順利的,人類的語言是有強烈規則性,每個字母的使用頻率並不均等,比方說母音a、e、i、o、u的使用頻率就是硬生生比別人高一大截,如果發現有五個字母的使用頻率異常高,那麼就可以猜測他們是a、e、i、o、u其中之一而後逐步破譯,接著搭配下圖索統計出來的字頻表便可以從中比對。
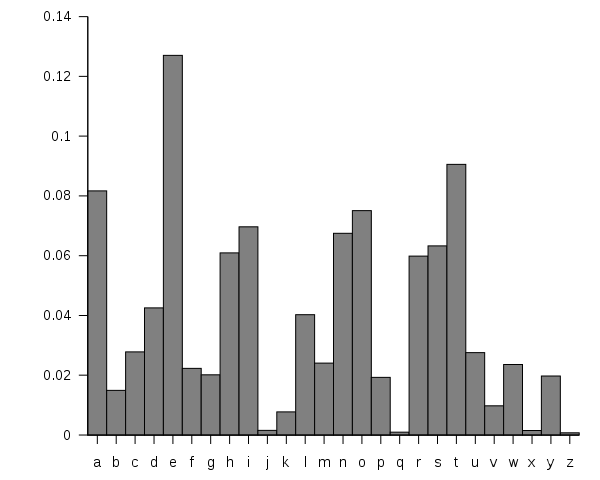
圖片來源:Wikipedia
雖然嘗試的次數多了些,但在搭配語言學與不斷嘗試的前提下仍然可以破譯,Monoalphabetic加密也不符合Kerckhoffs's principle。
Vigenère Cipher是Monoalphabetic加密一種威力加強版,既然Monoalphabetic加密只有一張表,那用很多張表來加密總行了吧?Vigenère Cipher便是產生很多張表格,並且彼此抽換,而Vigenère Cipher的金鑰指的就是目前這個字應該要用哪一張表格破譯,如果有ABCD四種Monoalphabetic表格,比較簡單的作法就是第一個字母用A表格、第二個字母用B表格、第三個字母用C表格、第四個字母用D表格、第五個字母用A表格....
但這樣利用語言本身重複的機率其實還是有辦法破譯,詳情限於篇幅可以參考這個PDF的16-21頁。

圖片來源:Wikipedia
順帶一提,這集的超智遊戲裏頭的每一種暗號都可以看做是一種表格,各種暗號(對照表)的交替使用能夠有效的增加破譯的難度,這一集裡頭渡久地用的方法其實跟Vigenère Cipher的精神一樣:不停地抽換暗號(編碼表)。
私心覺得超智遊戲還蠻好看的,有空的可以追追看。
One-Time Pad的作法跟Caesar加密類似,但具體鑰偏移幾個字是隨機決定的。比方說我們產生一個隨機偏移表:
24 7 21 5 18 ....
這張表就是One-Time Pad的金鑰,代表第一個字元我們要往後偏移24個、第二個字元我們要往後偏移7個、第三個字元我們要往後偏移21個、第四個字元我們要往後偏移5個、第五個字元我們要往後偏移18個....
如果產生的隨機金鑰長度跟訊息一樣,也就是每一個字元有自己的偏移與獨特的Monoalphabetic表格的話,理論上這One-Time Pad會因為密文與明文沒有任何統計上的關係而無法被任何數學或運算破解的加密法,你應該也可以發現經過One-Time Pad加密後的密文,明文可能是任何文字(例如密文是ABC,但因為每個字母的偏移量是隨機的,因此它有可能是car、cat、dog都有可能),因此也是唯一一種理論上無法被破解的密碼。但問題反而會在要如何安全、隨機地產生One-Time Pad、如何保護One-Time Pad的金鑰在傳送的過程中不會被幹走是主要的問題。
柵欄加密法指的是我們把明文根據某種排列方式或圖形排列後再重新寫出。舉例來說我們把Hello World分成上下兩行:

利用簡單的重新排序,就可以得到加密之後的密文:HWeolrllod,同時字序的結構也因此被打散了!
今天先把幾個古典加密的方法帶過去,明天我們來研究現代一點的密碼學!
到目前為止的文章都會放置在Github上,至於Caesar加密的程式碼則放在這裡、Monoalphabetic加密的程式碼放在這裡。
