前言

昨天最後稍微提到交大程式安全作業－猜數字遊戲和 PRNG，今天就順著繼續這個主題把他講清楚說明白，順便爭取一點時間想之後的文章.....QQ

Pseudo-Random Number Generator

為什麼不使用真正的亂數 ?

首先要知道一件事情：

目前靠純軟體無法取得真正的亂數

目前電腦發展至今，目前的行為都是由人類所定義好，因此要在電腦上取得亂數廣義來說只有兩種方式：

1. 亂數表
2. 透過 PRNG 取得亂數

但亂數表必須占用儲存空間，不可能擁有無限的儲存空間，因此理論上如果能取得夠多的亂數將亂數表給用完，下一個亂數就可以被預測；而 PRNG 是透過演算法來產生亂數，因此只要被知道是用哪一個演算法和必要條件 (seed)，也一樣可以預測接下來的亂數

現在如果需要在電腦上取得真正的亂數，一定要透過硬體的輔助，至於硬體取得的亂數是不是真正的亂數 (True Random Number)，問題就相當複雜，需要牽扯 entropy 的定義和各種物理知識，像是量子力學，甚至會探討到一些哲學問題，有興趣的可以參考 random.org 的說明

先假定透過透過硬體可以取得 True Random Number，但每次需要跟硬體溝通的 latency 就一定比不上從 PRNG 取得的速度，因此實際上還是會搭配 PRNG 使用，如昨天所提到的，比較簡單的做法就是透過 /dev/urandom 取得 seed 之後再餵給 srand 使用

Cryptographically Secure Pseudo-Random Number Generator

這邊引用 Allen Chou 大大在 HITCON 2014 <應用密碼學入門 >提及的亂數特性：

• 隨機性：看起來夠亂，沒有規律，所有數字分佈平均
• 不可預測性：無法從之前的亂數數列猜出下一個亂數的值
• 不可重複性：以後不可能再有同樣的數列

一般來說 PRNG 取得的亂數要能滿足 隨機性 (正式的名稱是 統計學偽隨機性)，簡單的說是產生夠多的亂數後，二進制的 1 和 0 數量會接近相等，滿足此條件人類體感上就會覺得是足夠隨機的亂數

CSPRNG 除了上述條件外，還必須滿足 不可預測性，以下是 wiki 的定義：

給定隨機樣本的一部分和隨機演算法，不能有效的演算出隨機樣本的剩餘部分

但無論是 PRNG 或 CSPRNG 都無法達到 不可重複性，只有 TRNG 才滿足三者的條件，BTW，要應用在密碼學上只有 CSPRNG 或 TRNG 得到的亂數才足夠安全

常使用的 PRNG

1. Linear Congruential Generator (LCG)
   • glibc rand 的實作採用此演算法，速度快但強度很弱
   • NOT CSPRNG
2. Mersenne Twister (MT)
   • 目前很多程式語言 Random 模組的實作方式，有不錯的速度且足夠大的 pool，適用於大部分情況
   • python: Random
   • php: mt_rand()
     • php 的 rand() 使用系統的預設函式，Linux 底下會等同於 glibc rand
   • NOT CSPRNG
3. Fortuna
   • FreeBSD 用以實作 /dev/urandom
4. arc4random
   • 從 stream cipher 的 key 取得亂數
     • iv 透過 kernel 從 hardware 上取得 noise
     • 早期基於 rc4，但現在改用 ChaCha20 實作
5. /dev/urandom
   • /dev/urandom 與 /dev/random 兩者都會從 hardware 取得亂數 entropy
   • 最大的差別是 /dev/random 會在 entropy 不夠時 block 住，等到足夠亂時才能得到亂數，/dev/urandom 則是會重複使用 entropy
   • 根據 man random(7) 的描述，只有在產生 secret key 時才建議讀取 /dev/random
   • Linux 4.8 之後改用 ChaCha20 實作/dev/urandom
     • https://lwn.net/Articles/686033/

小結

雖然說 PRNG 不夠安全，但 CSPRNG 和 TRNG 的使用成本太高，因此大家實務上還是會透過後者產生 seed 後，再結合 PRNG 使用，只要清楚了解自己使用了哪一套 PRNG 以及使用亂數的情境，就可以避免被預測到亂數而產生資安隱患

0x02: 30C3CTF 2013 Number 100 Guess

這道題是 2013 年參加 30C3CTF 初賽解的題目，也是人生中第一次解出作業或 Wargame 外的 CTF 的題目 XD
題目也是猜數字，但不只要猜中數字，還要連續猜對 10 次才行，是典型的預測 PRNG 的題目，詳細 write up 可以參考我的 blog: https://ddaa.tw/30c3ctf_2013_number_100_guess.html

題目是用 python 寫的 server，程式邏輯大致如下：

r = random.Random()
r.seed(os.urandom(16))

while 1:
  answer = str(r.getrandbits(64)
	guess = c.recv()
	if guess != answer:
	  guess_right = 0
	  c.sendall("Nope, that was wrong, correct would have been %s...\n" % answer)
	  continue
	guess_right += 1
	if guess_right < guess_limit:
	  c.sendall("Yes! That was correct, awesome...\n")
	  continue
c.sendall("You did it! The flag is: %s" % flag)

python 的 Random.getrandbits() 是使用 Mersenne Twister，透過 seed 初始化後會產生 624 個 state，每個 state 代表一個 32 bit 的數字，並可以產生出一個 32 bit 的亂數

因為題目是用 while loop 無止盡的執行，而且每次都會把 random 取得的結果印出來，因此我們可以收集足夠多的亂數來反推 MT 亂數產生過程的 state，具體作法如下：

1. 隨便猜錯一個數字，將 answer 拆成前半 a1 和後半 a2，分別是兩次 state 產生出來的亂數
2. 用 a1, a2 反推出 state 代表的結果 s1, s2
3. 重複 312 次，共得到 624 個state
4. 透過 state 計算之後會產生的亂數，至此我們已經可以預測接下來所有的答案

延伸閱讀

• HITCON CTF Web 300 Giraffe’s Coffee
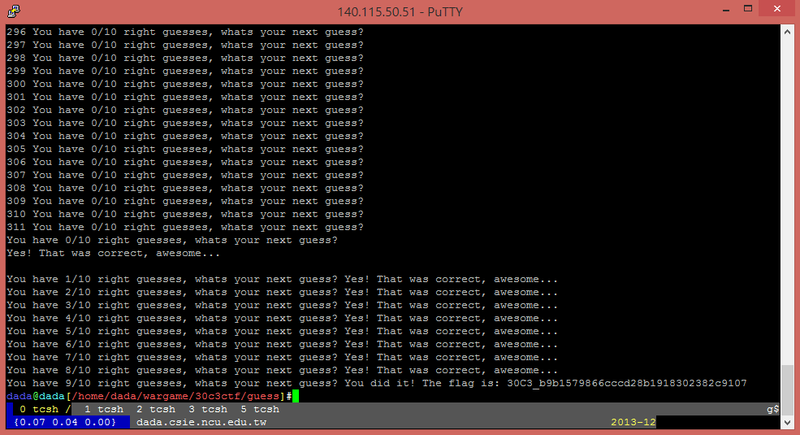
  • Orange 結合 Apache HTTP Server 和 php mt_rand 的特性，出了一題需要預測 PRNG 的題目
• https://www.openwall.com/php_mt_seed/
  • MT PRNG 懶人包，有相關的資安問題或 CTF 題目