Day23- project3 - 解經典9x9數獨問題

11th鐵人賽 python3

不明

2019-09-27 10:58:09

24099 瀏覽

分享至

路遙知碼力，日久練成精- 只要在程式之路鑽研的夠深，便能夠充分發揮程式碼的力量; 練習的日子夠久，便能夠練成寫出精簡代碼的能力。

首先討論一下昨天課後練習的答案:
(還沒看過題目的朋友歡迎點昨日題目傳送門)

def trans(state):
    return ['.'*state[i]+'Q'+'.'*(len(state)-state[i]-1) for i in range(len(state))]

如有其它想法也歡迎於留言區討論哦。

風靡全球的數獨介紹

今天要為大家介紹第三個程式小專題-數獨(sudoku)。
玩家需要根據格字內的數字推理出其它格字的數字。
例如這是一個數獨例題:

規則呢非常簡單:
在每一行、每一列、每一九宮格不重複的填上1~9九個數字即算完成，
例如這是此數獨的解答: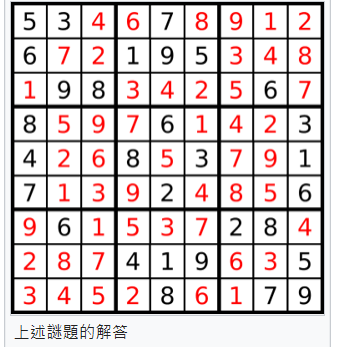

(參考資料: 數獨- 維基百科)

大概也因為這樣簡單又有趣的規則，
數獨算是全球流行的遊戲，
今天，教大家如何以程式來解決數獨謎題。
為了方便專注在探討解題邏輯，
我們假設拿到的數獨題目一定是合法的而且保證至少有一組解。

資料型態的選擇- 一維或二維陣列

首先是資料型態上的選擇，
我們要以什麼樣的資料型態來表示一個數獨題目呢?
大家可能覺得用二維陣列比較直覺，
但由於我們想要用類似於昨天解n皇后問題的遞迴搜索方法去解，
因此一維陣列可能還是方便串接(等一下實作程式會更有感覺)。
我們選擇用字串的一維陣列表示一個數獨題目，
"."表示還沒填上數字的空白格字，
例如此例表示維基百科上的數獨例題:

sudoku= \
["5","3",".",".","7",".",".",".",".",
 "6",".",".","1","9","5",".",".",".",
 ".","9","8",".",".",".",".","6",".",
 "8",".",".",".","6",".",".",".","3",
 "4",".",".","8",".","3",".",".","1",
 "7",".",".",".","2",".",".",".","6",
 ".","6",".",".",".",".","2","8",".",
 ".",".",".","4","1","9",".",".","5",
 ".",".",".",".","8",".",".","7","9"]

思考重點: 遞迴關係黑魔法

類似於昨天解n皇后問題的邏輯，
假設我們有一個神奇的函數solveSudoku(board)，
參數board是長度81的一維列表，表示一個數獨題目，
並且函數可以把所有滿足數獨規則的答案找出來，
那麼該如何建立遞迴關係呢?

首先，我們可以很暴力的從第一個空格開始填，
只要它沒有跟同一行、列、九宮格的數字相同都可以填，
把所有可能的答案收集起來就是了。

我們試著給程式邏輯打個草稿吧:

def solveSudoku(board):
    ans = [] #記錄所有可能的解答
    idx = 題目的第一個空格index
    exclude = 所有與board[idx]同一行、列、九宮格形成的集合
    for m in set('123456789')-excluded_nums: #嘗試填入不違規的數字
        ans += solveSudoku(board[:idx]+[m]+board[idx+1:])
    return ans

若你看懂的話，這邏輯甚至比昨天的n皇后問題還簡單吧?

細節思考: 判斷相同的行、列、九宮格

問題來了，給你兩個座標(介於0~80)，
你是否有辦法判斷它們是否在相同的行、列、九宮格呢?
我們使用一維列表，每個位置的座標如下所示:

 0  1  2  3  4  5  6  7  8
 9 10 11 12 13 14 15 16 17
18 19 20 21 22 23 24 25 26
27 28 29 30 31 32 33 34 35
36 37 38 39 40 41 42 43 44
45 46 47 48 49 50 51 52 53
54 55 56 57 58 59 60 61 62
63 64 65 66 67 68 69 70 71
72 73 74 75 76 77 78 79 80

你可以透過簡單的觀察規律得到兩個座標在同一行的關係式，
在同一行的位置index除以九的餘數都相等。
另外，在同一行的位置index除以九的商數都相等。
在同一九宮格的觀察較不直觀，直接告訴大家公式:
在同一九宮格的位置index，先除以九所得的餘數，
再除以三的商數會相等。
因此，我們可以定義出這幾三個函數，
分別判斷兩個座標位置i,j是否在同一列、行、九宮格:

def same_row(i,j): return (i//9 == j//9)
def same_col(i,j): return (i-j) % 9 == 0
def same_block(i,j): return (i//27 == j//27 and i%9//3 == j%9//3)

細節思考: 設定遞迴終止條件

前兩天有一再提醒讀者遞迴函數必須要有終止條件，
那本題中的終止條件是什麼呢?
當然就是沒有空格可以填的時候停止囉。
我們可以設idx = board.index('.') if '.' in board else -1，
讓idx表示題目中第一個空格位置，
如果已經沒有空格了則idx值設為-1，
當idx為-1我們就知道說函數該返回了。
依此想法，我們可以將solveSudoku函數完成:

def solveSudoku(board):
    ans = []
    idx = board.index('.') if '.' in board else -1
    if idx == -1: #解完了
        return [board]
    exclude = {board[j] for j in range(81) if same_row(idx,j) or same_col(idx,j) or same_block(idx,j)}
    for m in set('123456789')-exclude:
        ans += solveSudoku(board[:idx]+[m]+board[idx+1:])
    return ans

大功告成，附上完整程式碼

def same_row(i,j): return (i//9 == j//9)
def same_col(i,j): return (i-j) % 9 == 0
def same_block(i,j): return (i//27 == j//27 and i%9//3 == j%9//3)

def solveSudoku(board):
    ans = []
    idx = board.index('.') if '.' in board else -1
    if idx == -1: #解完了
        return [board]
    exclude = {board[j] for j in range(81) if same_row(idx,j) or same_col(idx,j) or same_block(idx,j)}
    for m in set('123456789')-exclude:
        ans += solveSudoku(board[:idx]+[m]+board[idx+1:])
    return ans

這邊依舊體現了python簡潔的魅力呢，
依舊短短十幾行就能夠解經典數獨問題了。

測試解數獨

或許讀者會好奇，
既然是從第一格嘗試所有可能性來填數字的解數獨，
會不會解開一個數獨要等到天荒地老啊?
我們直接以維基百科上的數獨例題做測試吧:

sudoku= \
["5","3",".",".","7",".",".",".",".",
 "6",".",".","1","9","5",".",".",".",
 ".","9","8",".",".",".",".","6",".",
 "8",".",".",".","6",".",".",".","3",
 "4",".",".","8",".","3",".",".","1",
 "7",".",".",".","2",".",".",".","6",
 ".","6",".",".",".",".","2","8",".",
 ".",".",".","4","1","9",".",".","5",
 ".",".",".",".","8",".",".","7","9"]
 
import time
tStart = time.time()#計時開始
print(solveSudoku(S))
tEnd = time.time()#計時結束
print("Total time= %f seconds" % (tEnd - tStart))

結果為:
[['5', '3', '4', '6', '7', '8', '9', '1', '2', '6', '7', '2', '1', '9', '5', '3', '4', '8', '1', '9', '8', '3', '4', '2', '5', '6', '7', '8', '5', '9', '7', '6', '1', '4', '2', '3', '4', '2', '6', '8', '5', '3', '7', '9', '1', '7', '1', '3', '9', '2', '4', '8', '5', '6', '9', '6', '1', '5', '3', '7', '2', '8', '4', '2', '8', '7', '4', '1', '9', '6', '3', '5', '3', '4', '5', '2', '8', '6', '1', '7', '9']]
Total time= 0.156252 seconds
可以看到程式真的把數獨解開了，
而且不到一秒就解了，
沒有想像中的那麼耗時，
大概是因為實際亂填數字的時候，
容易因不合規則而提早結束搜索吧。
雖然我們的程式能夠窮舉所有解，
但坊間的數獨大多是設計成有唯一的解，
一般來說，倒也不必太擔心可能性太多而時間爆炸的問題。

課後練習- 視覺化印出9x9數獨的解

目前我們可以看到已經能夠程式已經能夠解開數獨了，
但是這樣
[['5', '3', '4', '6', '7', '8', '9', '1', '2', '6', '7', '2', '1', '9', '5', '3', '4', '8', '1', '9', '8', '3', '4', '2', '5', '6', '7', '8', '5', '9', '7', '6', '1', '4', '2', '3', '4', '2', '6', '8', '5', '3', '7', '9', '1', '7', '1', '3', '9', '2', '4', '8', '5', '6', '9', '6', '1', '5', '3', '7', '2', '8', '4', '2', '8', '7', '4', '1', '9', '6', '3', '5', '3', '4', '5', '2', '8', '6', '1', '7', '9']]
以一個長度81的一維陣列表示一組解，
對讀者來說並不那麼直覺，
我們希望將數獨的解答九個字一行的印出來，
(這件事不一定要用函數包裝起來，你能完成這項功能就好)
例如:

['5', '3', '4', '6', '7', '8', '9', '1', '2']
['6', '7', '2', '1', '9', '5', '3', '4', '8']
['1', '9', '8', '3', '4', '2', '5', '6', '7']
['8', '5', '9', '7', '6', '1', '4', '2', '3']
['4', '2', '6', '8', '5', '3', '7', '9', '1']
['7', '1', '3', '9', '2', '4', '8', '5', '6']
['9', '6', '1', '5', '3', '7', '2', '8', '4']
['2', '8', '7', '4', '1', '9', '6', '3', '5']
['3', '4', '5', '2', '8', '6', '1', '7', '9']

讓我們能夠更方便的看出來每個數字填的位置。
我們明天見囉。