哈囉~ 大家好，今天分享一個有趣的棋盤問題。

這個問題也是從西洋棋延伸而來的問題，
給你一個西洋棋盤，
如何讓騎士從一個點出發，不重複的走遍整個西洋棋的棋盤?

騎士的走法是走「日」字形(相當於象棋馬的走法)，
例如: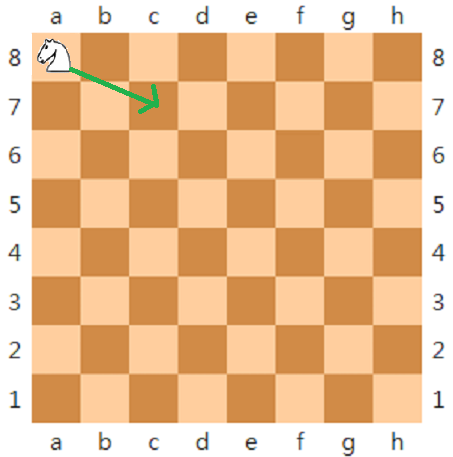

譬如說以下表示騎士從最左上角出發，走遍棋盤的一組解(數字代表順序)

 1  4 27 42 53  6  9 12
26 43  2  5 46 11 52  7
 3 28 45 54 41  8 13 10
44 25 58 61 64 47 40 51
29 60 55 48 57 50 63 14
24 19 22 59 62 37 34 39
21 30 17 56 49 32 15 36
18 23 20 31 16 35 38 33

本篇探討如何用程式把任意一組解找出來
(我們只想找一組解，不想窮舉所有解)

遞迴思路

這邊先給一支範例:

dirs = [(1, 2), (2, 1), (-1, 2), (-2, 1), (1, -2), (2, -1), (-1, -2), (-2, -1)] # 馬步的八個方向
find = False #全域變數，當find=True時停止搜索
chessboard = [[0]*8 for i in range(8)] #二維列表表示一個西洋棋的棋盤
chessboard[0][0]=1 #初始條件

# 默認參數curstep表示現在第幾步
def Move(pos, curstep=1):
    chessboard[pos[0]][pos[1]]=curstep  #設定棋步
    if curstep==64: #一旦找到一組解，印出解答並設find=True
        for i in range(8):
            print(' '.join([f"{chessboard[i][j]:2d}" for j in range(8)]))
        global find
        find = True 
    else:
        for d in dirs: #檢查下一步我可以走的八個方向
            nextPos = [pos[0]+d[0], pos[1]+d[1]]
            if not find and 0<=nextPos[0]<=7 and 0<=nextPos[1]<=7 and chessboard[nextPos[0]][nextPos[1]]==0:
                Move(nextPos, curstep+1)      
    chessboard[pos[0]][pos[1]]=0 #撤銷棋步


iniPos = (0,0) #初始座標
Move(iniPos)

利用深度搜索，每次嘗試走棋盤的八個方向，
用參數curstep表示現在走到第幾步了，
如果curstep==64表示棋盤填滿了就印出答案，
然而實際執行程式後，
會發現好像等到天荒地老程式也跑不出結果，
會是邏輯錯嗎?

我們嘗試把程式中的if curstep==64:改成if curstep==50:

 1  0 49  0 23  0  0 26
50  0  2 47 42 25 22  0
 0 48 43 24  3 18 27 20
 0  0 46 41 28 21  4  9
 0 40 29 44 17 10 19 12
 0 45 36 33 30 13  8  5
39 34 31 16 37  6 11 14
 0  0 38 35 32 15  0  7

我們讓棋盤不必整個填滿，
在棋盤上走50步並印出，
這時真的很快跑出一組解了

我們發現一個問題，
未限制深度搜索中騎士走的方向，
騎士在中間亂走，導致角落的格子最後容易走不到

技巧: 角落的格子優先走

這支程式可以這樣優化，
因為角落的棋格感覺上比較不容易走到，
因此愈接近角落的格子其實可以先搜索，
讓程式更容易找到解

我們可以為每個格子定一個「邊緣分數」，
取x, y座標靠近邊界的距離和，
愈靠近角落的格子分數愈低

譬如說我們看西洋棋盤，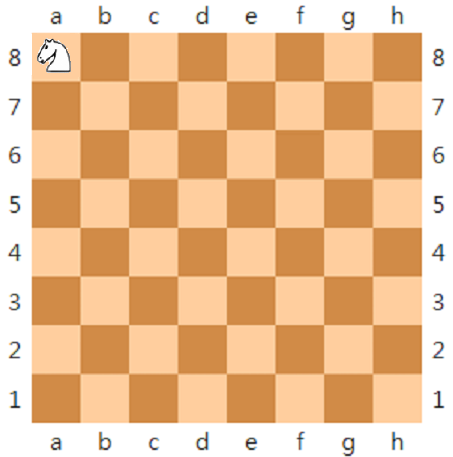

例如說座標h1的格子在角落為0分，
座標g3距離下邊界2格，距離右邊界1格，
因此g3的「邊緣分數」=2+1=3。
分數愈低表示格子愈接近角落，就要愈優先搜索

優化後的程式如下:

dirs = [(1, 2), (2, 1), (-1, 2), (-2, 1), (1, -2), (2, -1), (-1, -2), (-2, -1)] # 馬步的八個方向
find = False #全域變數，當find=True時停止搜索
chessboard = [[0]*8 for i in range(8)] #二維列表表示一個西洋棋的棋盤
chessboard[0][0]=1 #初始條件

# 判斷一個座標是否可走
def valid(pos):
    return 0<=pos[0]<=7 and 0<=pos[1]<=7 and chessboard[pos[0]][pos[1]]==0
    
# 計算一個格子座標的「邊緣分數」
def value(pos):
    return min(pos[0],7-pos[0])+min(pos[1],7-pos[1])

# 默認參數curstep表示現在第幾步
def Move(pos, curstep=1):
    chessboard[pos[0]][pos[1]]=curstep  #設定棋步
    if curstep==64: #一旦找到一組解，印出解答並設find=True
        for i in range(8):
            print(' '.join([f"{chessboard[i][j]:2d}" for j in range(8)]))
        global find
        find = True 
    else:
        #nextPos是下一步可以走的座標位置，依「邊緣分數」排序
        nextPos = [[pos[0]+d[0], pos[1]+d[1]] for d in dirs] 
        nextPos = sorted(filter(lambda x: valid(x), nextPos), key= lambda x: value(x))
        for p in nextPos: #檢查下一步我可以走的八個方向
            if not find:
                Move(p, curstep+1)      
    chessboard[pos[0]][pos[1]]=0 #撤銷棋步


iniPos = (0,0) #初始座標
Move(iniPos)

順利跑出一組解如下:

 1  4 27 42 53  6  9 12
26 43  2  5 46 11 52  7
 3 28 45 54 41  8 13 10
44 25 58 61 64 47 40 51
29 60 55 48 57 50 63 14
24 19 22 59 62 37 34 39
21 30 17 56 49 32 15 36
18 23 20 31 16 35 38 33

推廣: 解nxm棋盤的馬踏棋盤問題

上述示範8x8棋盤的馬踏棋盤問題如何解，
但是推廣至一般大小棋盤的解法是一樣的，
這邊包裝成class，
只要輸入棋盤大小及初始位置就能解了。

class HorseWalk:

    def __init__(self, r, c):
        self.r = r
        self.c = c
        self.board = [[0]*c for i in range(r)] #二維列表表示一個西洋棋的棋盤
        self.dirs = [(1, 2), (2, 1), (-1, 2), (-2, 1), (1, -2), (2, -1), (-1, -2), (-2, -1)] # 馬步的八個方向
        self.find = False #全域變數，當find=True時停止搜索

    # 判斷一個座標是否可走
    def valid(self, pos):
        return 0<=pos[0]<=self.r-1 and 0<=pos[1]<=self.c-1 and self.board[pos[0]][pos[1]]==0
        
    # 計算一個格子座標的「邊緣分數」
    def value(self, pos):
        return min(pos[0],self.r-pos[0]-1)+min(pos[1],self.c-pos[1]-1)

    # 默認參數curstep表示現在第幾步
    def Move(self, pos, curstep=1):
        self.board[pos[0]][pos[1]]=curstep  #設定棋步
        if curstep==self.r * self.c: #一旦找到一組解，印出解答並設find=True
            for i in range(self.r):
                print(' '.join([f"{self.board[i][j]:2d}" for j in range(self.c)]))
            self.find = True 
        else:
            #nextPos是下一步可以走的座標位置，依「邊緣分數」排序
            nextPos = [[pos[0]+d[0], pos[1]+d[1]] for d in self.dirs] 
            nextPos = sorted(filter(lambda x: self.valid(x), nextPos), key= lambda x: self.value(x))
            for p in nextPos: #檢查下一步我可以走的八個方向
                if not self.find:
                    self.Move(p, curstep+1)      
        self.board[pos[0]][pos[1]]=0 #撤銷棋步


iniPos = (0,0) #初始座標
solver = HorseWalk(6,6)
solver.Move(iniPos)

一些發現:
棋盤太小的時候好像會沒有解，
譬如說3x5, 4x4我都沒搜到解。
目前我程式最大可以搜到9x10棋盤的一組解，
超過的話計算量好像還是有點太大。

 1  4  7 10 43 86 63 36 41 38
 8 11  2  5 62 75 42 39 64 35
 3  6  9 44 85 78 87 74 37 40
12 45 58 61 80 83 76 89 34 65
57 60 81 84 77 88 79 68 73 90
46 13 56 59 82 69 72 31 66 33
19 16 49 70 55 52 67 28 25 30
14 47 18 21 50 71 54 23 32 27
17 20 15 48 53 22 51 26 29 24