我這個人不管是數學還是程式最不喜歡的就是遞迴，每次都把自己搞得暈頭轉向
而遞迴這個概念源自於分怡法A.K.A Divide and Conquer
簡單來說就是把一個龐大的問題分割成一小部分相似的中等大小的問題，
然後再把這些中等大小的問題再分割成更小部分相似的小問題，
然後再把這些小問題用相似的function去解決，最後處裡完這個大問題。

如果在一個電腦的程式中，一個函式在執行時會不斷呼喚自己，這時候
就會認為這個程式有遞迴的性質。而為了避免它無窮無盡的呼喚自己，通常都
會設計一個終止條件。

1.階乘
示範一個階乘函數
階乘就是n! = 1x2x3...xn
我們只需要一個 n 次的 for loop 就可以解決這個問題

def factor_loop(n):
   factor = 1
   for i in range(1,n+1):
       factor *= i
   return factor

print(factor_loop (5))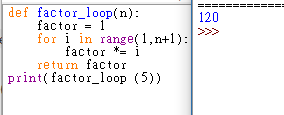

**2.費氏數列 **
費氏數列也是遞迴概念，所謂的費波那契數列，
指的是一個數列，每一項都等於他的前兩項的和，
也就是說第 n 項等於第 n-1 項以及第 n-2 項的和。
數學上的公式是這樣
f(0) = 0, f(1) = 1
f(n) = f(n-1) + f(n-2), n>=2
我們想要求得的是第 n 項的值，我們的函式參數為整數 n
，它每一次都會呼叫以 n-1 為參數以及 n-2為參數的函式，
並且將他們的回傳值相加起來再 return 。
但若參數值為 1 或是 0 ，根據費氏數列的定義，我們就要直接回傳 1 和 0(根據公式)
所以運用我們之前學過的elif來寫函式

def fibonacci(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fibonacci(n-1) + fibonacci(n-2)