前言

初接觸機器學習時，常會給幾個效能衡量指標搞得一個頭兩個大：

1. 混淆矩陣(Confusion Matrix)。
2. 準確率(Accuracy)、精確率(Precision)、召回率(Recall)、F1 Score、真陽率(True Positive Rate)、假陽率(False Positive Rate)...。
3. ROC/AUC 曲線

要衡量演算法的效能，不就是算正確的個數佔全體樣本的比例就好了嗎? 為甚麼發明一堆的比率，搞死一堆腦細胞呢?以下筆者試著用圖表及簡短的說明，釐清一些觀點，囿於才疏學淺，不夠精準的地方，還請不吝指正。

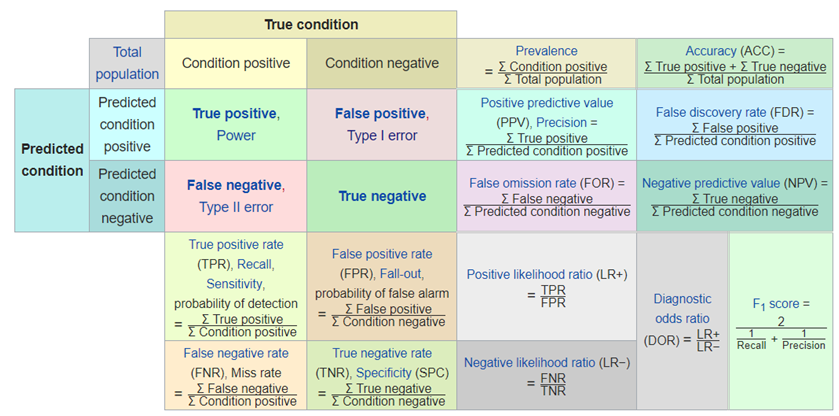
圖. 混淆矩陣(Confusion Matrix)及相關效能衡量指標，資料來源：Confusion matrix -- Wiki

混淆矩陣(Confusion Matrix)

看到上圖，就頭皮發麻了，哪記得那麼多公式啊，不急，我們先拿掉周圍的比率，只留下左上角，並且翻譯為中文，如下圖：

圖. 混淆矩陣(Confusion Matrix)

圖中四格(tn, fp, fn, tp)代表的意義如下，口訣是先解讀第二個字母，再解讀第一個字母：

1. tp：預測為陽性(p)，預測正確(t)。
2. tn：預測為陰性(n)，預測正確(t)。
3. fp：預測為陽性(p)，預測錯誤(f)。
4. fn：預測為陰性(n)，預測錯誤(f)。

其中 fp 又被稱為『型一誤差』(Type I Error)，也稱為 α error，以假設檢定來說，當H0(虛無假設)為真時，預測 H1 為真。反之，fn 又被稱為『型二誤差』(Type II Error)，亦稱為 β error，以假設檢定來說，當H0為假時，預測 H1 為假。

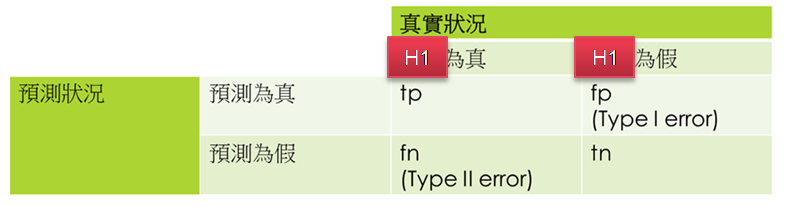
圖. 假設檢定之混淆矩陣(Confusion Matrix)

混淆矩陣計算範例

實際計算很簡單，Scikit-Learn 直接支援混淆矩陣的計算，只要把真實值(Ground Truth)及預測值(Prediction)放入參數中，就搞定了。

from sklearn.metrics import confusion_matrix

actual = [1, 1, 0, 1, 0, 0, 1, 0, 0, 0]
predicted = [1, 0, 0, 1, 0, 0, 1, 1, 1, 0]
tn, fp, fn, tp = confusion_matrix(actual, predicted).ravel()
print(tn, fp, fn, tp)

準確率、精確率(Precision)、召回率(Recall)、F1 Score

了解混淆矩陣後，就可依據 tn, fp, fn, tp 計算各式比率，以衡量模型的效能，相關公式都很簡單，如下：
準確率（Accuracy）= (tp+tn)/(tp+fp+fn+tn)
精確率（Precision）= tp/(tp+fp)，即陽性的樣本中有幾個是預測正確的。
召回率（Recall）= tp/(tp+fn)，即事實為真的樣本中有幾個是預測正確的。
F1 = 2 / ( (1/ Precision) + (1/ Recall) )，即精確率與召回率的調和平均數。

其他比率公式請參看圖一。

一般情況下，我們只要使用準確率(Accuracy)衡量模型的效能即可，就是『預測正確的比率』，即猜對的個數(tp+tn) / 全部樣本數。但是，當訓練資料的目標變數不平衡(imbalance)時就要小心了，以下以檢驗設備為例詳細說明。

假設有1000人接受癌症檢查，實際上有2人患有癌症，如果醫療檢驗設備檢查出3人為陽性，則其準確率為 999/1000=99.9%，這結果大家應該都很滿意，但是，如果有一天這台設備故障了，同樣檢查1000人，無人為陽性，這時準確率為 998/1000=99.8%，這結果大家應該很傻眼吧。為了矯正這個現象，我們使用精確率（Precision）計算看看：

1. 未故障： 2/3
2. 故障時：0/0，無法計算。
   應該就可以發現設備有問題了。

留個問題給讀者，為什麼不考慮陰性的樣本?

再舉一個例子，根據統計美國每年有1000萬人次出入境，假設有10個恐怖份子試圖闖關，海關有抓到5個嫌疑犯，如果以準確率計算，(1000萬 - (10-5))/1000萬=99.9999..%，準確率高得嚇人，但是美國政府會滿意嗎? 事實上有一半的恐怖份子沒抓到，這時如果改用召回率（Recall）計算，5/10=50%，就合理多了。

結論

以上個人心得希望能有助於觀念的釐清，以較輕鬆的方式舉例說明，如有失當，還請各位先進不吝指正，下次接著談另一個很難搞的效能指標 -- ROC/AUC。