早在30年前，神經網路技術早就已經存在，並且盛行過一段時間，不過在1980~2000年左右轉而流行支援向量機(SVM)。最主要原因是當時能夠搭建的神經網路層數不多，導致神經網路所能學習到的特徵有限，造成模型Performance不佳，而這些層數不多的網路稱為淺層神經網路。而近年來，隨著電腦的進步，以至於能搭建更龐大的神經網路，使電腦可以被訓練得更多。

什麼是Linear regression
簡單來說，找出符合資料規律的直線，即為線性迴歸。線性迴歸主要利用自變數(X)來預測依變數(Y)。一般來說，線性回歸有許多方式求解，像是我們在大學有學過公式解。其中公式解其實就利用最小平方法來求解。而最小平方法其目的就是希望透過觀察值與預測值差異的平方和最小化。因此透過loss function的設定及微分求導，可以得到一般所看到的公式解。
而當資料太大時，公式解可能就不會是一個有效率的解法，因此，一般來說都會改用gradient desent求解找出最佳的權重。

激活函數
激活函數(Activation fuction)，關於這個函數你也不用想的太複雜，你就把他當成三角函數，現在大多人都用ReLU函數，他可以有效的避免梯度消失問題。
而這個函數的用法就把小於0的全部歸零，如果大於零的就不理會他，看到這大家一定想說是在[哈囉!]，但不能否認的ReLU是目前最好用的激勵函數之一。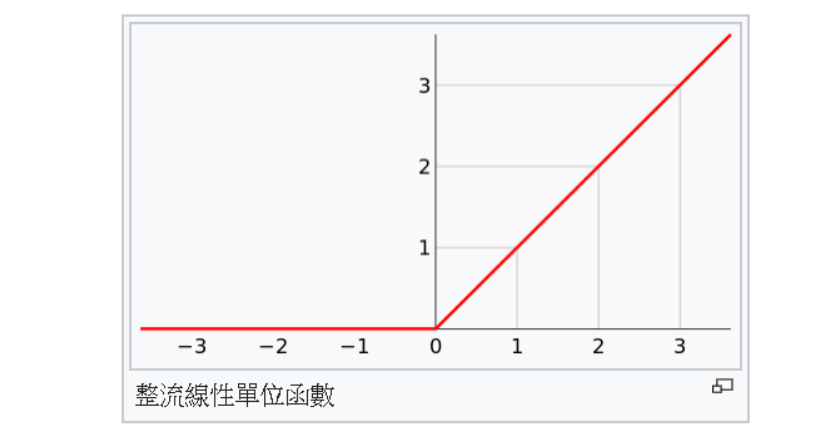

神經網路的原理
神經網路可以將它拆成輸入層、隱藏層和輸出層，網路中每一層都有許多神經元，神經元與神經元的連結都要倚賴權重和偏差
就像我們要算段考成績一樣，首先我們先放入3個神經元做為輸入層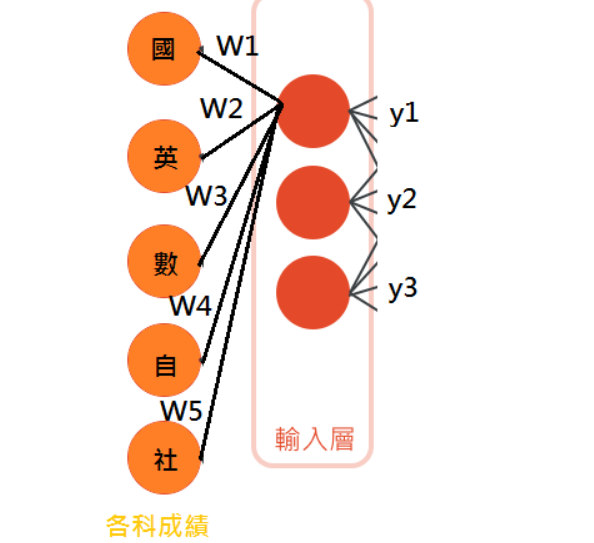

所以簡單來說 y1 =w1x1+w2x2+w3x3+w4x4+w5x5 裡面的w就代表權重，而這種簡單的輸出，因為只有相加和相乘所以它必然是個線性的計算，所以我們會想透過激活函數，比如上面提到的ReLU來讓它變成非線性的，進而解決我們日常生活大多的非線性的問題。
函式會變成 y1 =ReLU(w1x1+w2x2+w3x3+w4x4+w5x5)
在輸入層每個神經元都會接收到各科成績，但是他們所帶有的權重矩陣(w1,w2,w3,w4,w5)是不同的。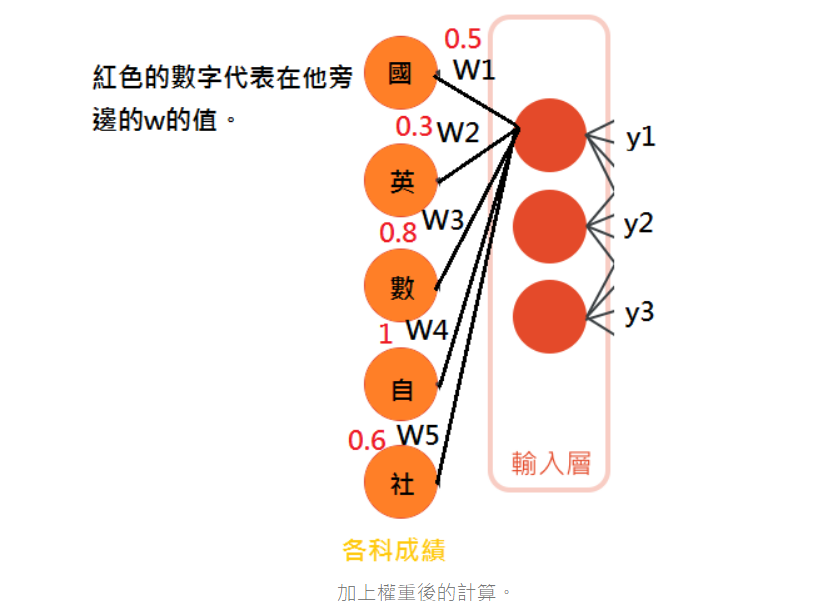

紅色的數字就代表神經元對於各科成績的重視程度，各科成績會被承上這個加權值。
每個神經元都透過不同的權重矩陣來得到不同的認知，每一個權重矩陣都是完全隨機的，這讓每個神經元一開始都有不同的加權傾向，就像有些神經元可能會重視國文，有些重視數學。
也因為會有很多的隱藏層，所以我們的神經元會把輸入值加總進行計算，下一層的神經元也會把上一層的輸出值加總進行運算。
這一篇只是一些基本的小基礎，下一篇我會介紹關於實作方面要注意的事情和如何神經網路權重更新和學習率。
參考
https://medium.com/%E6%A9%9F%E5%99%A8%E5%AD%B8%E7%BF%92%E7%9F%A5%E8%AD%98%E6%AD%B7%E7%A8%8B/dnn-%E6%B7%B1%E5%BA%A6%E7%A5%9E%E7%B6%93%E7%B6%B2%E8%B7%AF-%E7%9A%84%E5%85%A8%E9%9D%A2%E8%AA%8D%E8%AD%98-ad50aa531205
https://ithelp.ithome.com.tw/articles/10218584