在資料結構中，有一種由點和邊組成的稱為圖（graph）。樹（tree）就是圖的一種，但圖的變化性又更高。樹是由上而下的結構，有階層性存在，圖就相對平面。我們可以把點想像成城市，邊就是城市間的路徑。不一定每兩座城市間都有路徑，所以點和點之間有時候是不能抵達的，但如果 A 能走到 B，B 又能走到 C，A 就能透過中介點抵達 C。另外，有時候邊是有方向性的，就像路有單行道一樣，所以有時候 A 能走到 B，B 卻沒辦法走回 A。

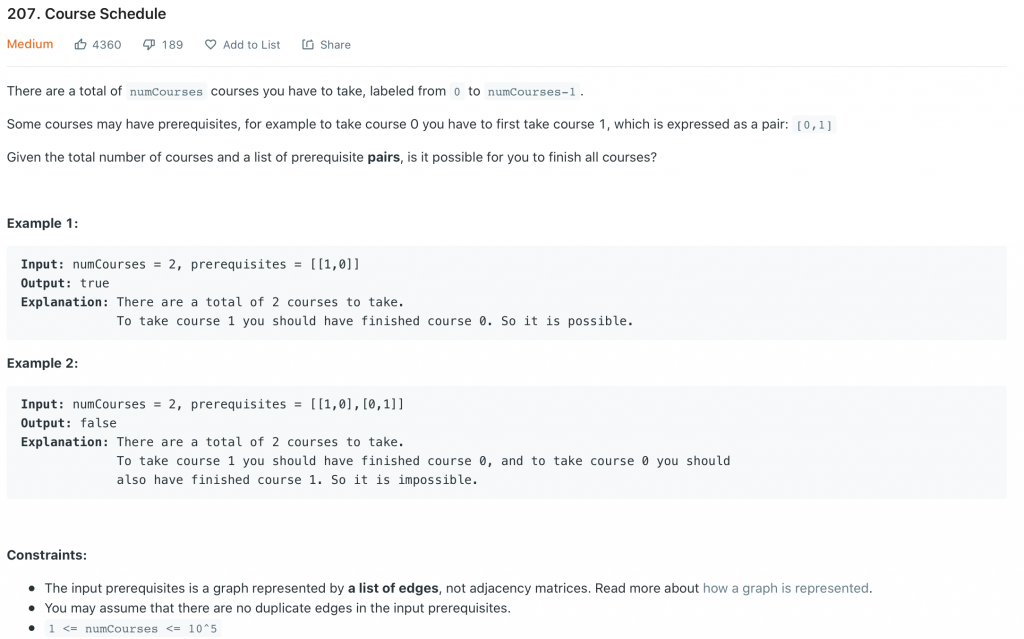
有了基本概念之後，接著就能看題目了。這個題目的輸入是一系列的課程與條件，每門課有各自的先修條件，有些課必須排在另一些課前面，像大學課程會擋修一樣。我們的任務就是：判斷能不能在給定的條件下排出一個合理的順序。簡單來說，如果這些條件是合乎邏輯的，我們就能排出一個滿足所有條件的序列；但如果條件彼此矛盾，像 A 要求先修過 B，B 又要求先修過 A，那怎麼排都會導致問題，這種試圖滿足所有條件的排列法就是拓撲排序。

在這題中，我們首先檢視每個條件，並計算每門課要求的先修課數量。如果有些課的先修條件是 0，這些課就會排在最前面，當成基礎課程。假設基礎課程有 A、B、C，緊接著就看，哪些課要求的先修課包含這三門，以及在修完這三堂課後，是否滿足了課程條件。沒有滿足的就持續擱置，滿足了就把第二批課程排進來。之後，再進一步確認先修條件包含第二批課程的高階課程狀況，然後持續排序。假如條件有矛盾狀況，那些課就永遠不會被排到修課序列中。所以我們能排出條件下可行的順序，最後再拿出排序，確認是否修完所有課程就結束了。

// javascript
var canFinish = function(numCourses, prerequisites) {
  const condition = Array(numCourses).fill().map(item => [])
  const degree = Array(numCourses).fill(0)
  const order = []
  
  for(item of prerequisites) {
    condition[item[1]].push(item[0])
    degree[item[0]] += 1
  }
  
  for(let i = 0; i < numCourses; i++) {
    if (degree[i] == 0) order.push(i)
  }
  
  for (index of order) {
    for (follower of condition[index]) {
      degree[follower] -= 1
      if (degree[follower] == 0) order.push(follower)
    }
    index += 1
  }
    
  return order.length == numCourses
  
};