2-5 賭博嘛!玩玩就好

咖啡廳裡，瀰漫著剛加熱完的奶香與打磨到一半的咖啡碎豆香，雖說是來到咖啡廳，但飛哥與小博卻都沒有點咖啡相關的飲品，只是點了些平常愛吃的甜點就馬上進入正題。

「上次不是跟你說過常態分佈嗎?」飛哥說道。

「有是有但我也不大記得啦，哈哈哈!」剛哥乾笑了三聲，邊抓著頭顯得有些不好意思。

「以兩顆骰子為例，點數和最小是2，點數和最大是12，但是你看，愈中間的數字他的組合愈多出現機率愈大，也就是說愈極端的數字總和出現的機率愈小」飛哥切了塊重乳酪蛋糕放進嘴哩，露出滿足的表情。

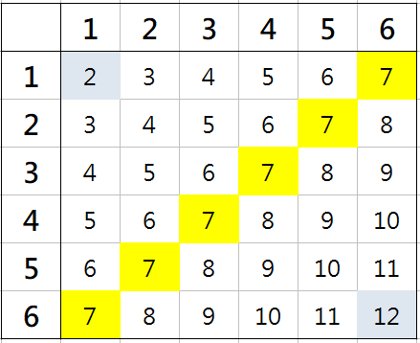
「那我玩的三顆骰子的骰寶又怎麼辦?」剛哥露出疑惑的表情。

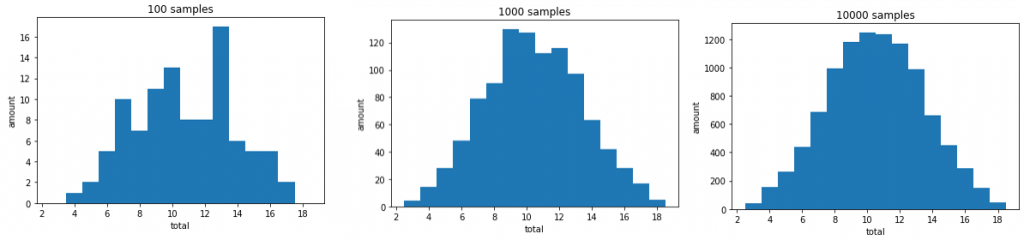
「你看下面這三張圖，剛剛我說了，一個數字有愈多組合，那丟出它的次數理論上比較多，但你有沒有發現，我重複丟100次骰子的點數分佈並不是很漂亮的鐘形分佈，但是隨著我丟的次數從100上升到10000的過程中，這個常態分佈的鐘型形狀就漸漸出現了，這就是所謂的『中央極限定理』啦!當我的樣本數夠大時，我樣本的分佈就會趨近於完美的常態分佈。」飛哥鉅細靡遺地解說著。

「還有啊，像我們一般人的身高體重、一個縣市的各人薪水，到電池耗用的時長、機車的使用壽命等等，這些如果資料收集的夠多的話，都可以發現它是一個常態分佈。還有很多不同的分佈型態這邊我就先不說了，反正一下子講太多你也會忘記。」飛哥又切了一塊蛋糕放入口中。

「照這樣來看，賭場內部應該還是存在著能讓我勝利的機率!」剛哥眼睛發亮的說著。
飛哥嘆了口氣:「有是有，不過要是這麼簡單的話，應該也輪不到你，別人花了畢生積蓄都傾家蕩產，你口袋的錢可能還不夠賠呢!聽我一句話吧!偶而玩玩到無妨，但是你真的投入大量的金額進去時，就準備睡公園吧!」

小博在一旁聽得津津有味，看著眼前兩位都是經歷過大風大浪的人，想著不知未來自己的人生又會有怎樣的際遇呢?

Python程式時間

import numpy as np
import pandas as pd
import random
import matplotlib.pyplot as plt

times=10000
d = [None] * times
for i in range(times):
    a=random.choice(dice);b=random.choice(dice);c=random.choice(dice)
    d[i]=a+b+c
x = np.arange(3,20,1) #設定直方圖有幾條bar
plt.hist(d,bins=x,align='left')
plt.title("10000 samples");plt.xlabel("total");plt.ylabel("amount")
plt.show()    
    
import collections, numpy
collections.Counter(d) #計算array中的數字各出現幾次

後記: 之前去過一次澳門的賭場見見世面，最吸引我的不是百家樂、角子老虎機，而是「輪盤」，記得我花了好幾個晚上去研究各種偏門啊手法啊，最後得出的結論是，每個輪盤在製作上不可能完美無瑕因此還是會偏向某些區域，每個荷官也有自己常用的手法，如何在短時間內找出這些規律並加以利用，才是最需要的技能，方法是活的，不是光靠幾個技巧就能縱橫賭場，不過還是多說一句『少賭為妙~小賭怡情，大賭傷心』。