記錄學習內容。看網路上大大們的文章和影片，做些紀錄。
以下內容大多來自網路上大大們的文章。
還不了解，內容可能有錯誤。

之前有紀錄排序的程式 ，現在學習排序的一些觀念

java，quicksort、Counting Sort和c++ ，mergesort、Heap Sort和 js ，Shell Sort、Radix Sort
https://ithelp.ithome.com.tw/articles/10219345

主要是看
[演算法] 排序演算法(Sort Algorithm)
http://notepad.yehyeh.net/Content/Algorithm/Sort/Sort.php

quicksort

Best Case：Ο(n log n)

2.3.3 Recurrence Relation [ T(n)= 2T(n/2) +n] #3
https://www.youtube.com/watch?v=1K9ebQJosvo&list=PLDN4rrl48XKpZkf03iYFl-O29szjTrs_O&index=26&ab_channel=AbdulBari

Worst Case：Ο(n * n)

2.1.2 Recurrence Relation (T(n)= T(n-1) + n) #2
https://www.youtube.com/watch?v=IawM82BQ4II&list=PLDN4rrl48XKpZkf03iYFl-O29szjTrs_O&index=20&ab_channel=AbdulBari

Average Case：Ο(n log n)

空間複雜度(Space Complexity)：Ο(log n) ~ Ο(n)

因遞迴的深度而異
Best Case： Ο(log n)
遞迴呼叫的深度為log n
Worst Case： Ο(n)
遞迴呼叫的深度為n-1

穩定性(Stable/Unstable)：不穩定(Unstable)

因為 i 會不斷 往 右邊走 ，找到 比 3 大 的值 才停下來
J會不斷往左邊走 ，直到 有 小於等於3 的值 才停下來 。
停下來之後 ，兩個值 互換位置 。

I和j 繼續走 ，走到 i 超過 j 的時候 (兩軍交會過了)，就停下來。
然後 互換 j索引的值 和 pivot 索引的值

會發現是unstable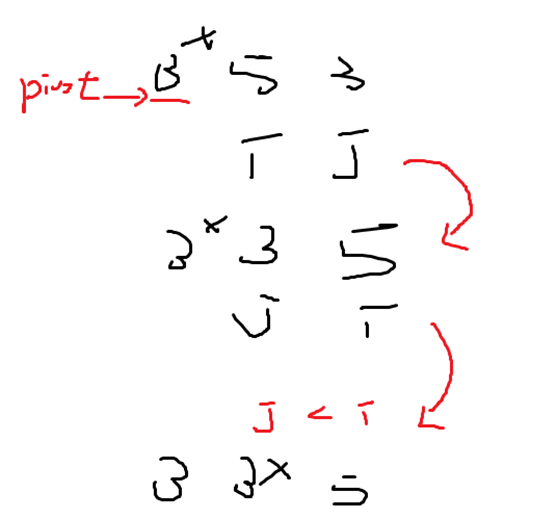

接著來看:
QuickSort
https://www.geeksforgeeks.org/quick-sort/

教學裡 的寫法 ，跟前面想的方法，有些不一樣:

i  從 第 -1 項開始 。
j  從 第 0 項 開始 ， 如果 j 索引的值  <  pivot 索引的值 。

i++   後 ，j索引的值  就會跟 i索引的值交換 。
就會造成 i索引 左邊的數字 都比  pivot 索引的值 小

最後 把 pivot 索引的值  放到 i+1 索引的地方  。

跟  i 在0索引 直到 找到大的才停下 、
j 在  最右邊(陣列長度索引)  直到 找到小於等於的 才停下 交換 ，效果一樣?(不知)

用這個方法，畫畫看圖(還是不穩定):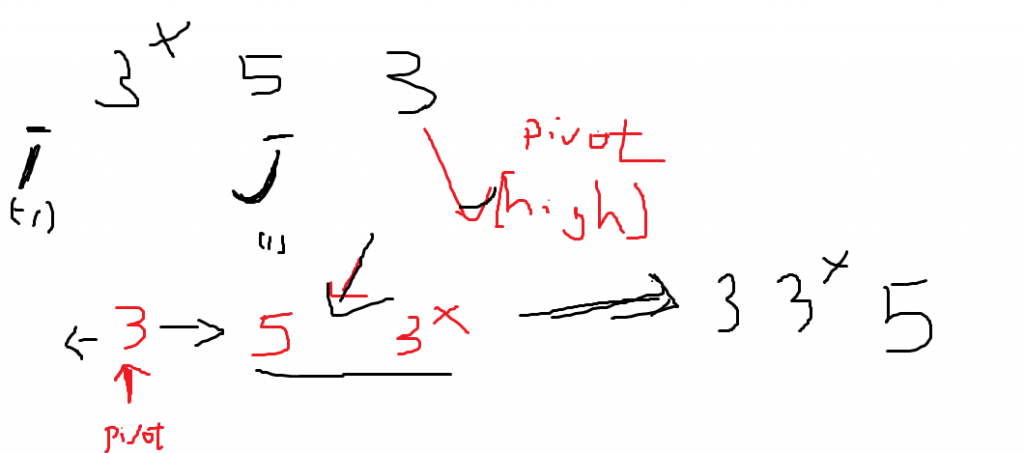

看這個 Dutch National Flag Algorithm (荷蘭國旗 三種顏色):

3-Way QuickSort (Dutch National Flag)
https://www.geeksforgeeks.org/3-way-quicksort-dutch-national-flag/

把數字分為 比5小 、5 、比5大 ，三種狀況

原本的想法是 :

從最左邊 找 比5 大的停下
從最右邊 找 比 5 小的停下
之後交換 。

或是 只從 最左邊開始走 ， 走到比 比5 小的停下 ，
跟 最左邊交換 ， 這樣左邊都是比5小的了

Dutch National Flag Algorithm 的想法是 :

Low 代表 最左邊 ，high代表最右邊

如果 這個數字 比 5 小， 就放到最左邊 ，然後Low++
如果 這個數字 比 5 大， 就放到最右邊 ，然後high—
最後 自然也會分成3塊 。

來看程式部分
多了兩個變數 i和j :

像是現在pivot值是5 ，每一輪都會把5放到正中間 ， 之後下一輪 ，取 5的左半部 和 右半部 ，繼續排序。
所以用這個演算法 ， 如果數列是 5 5 5 5 5 5 5 5 5 5 5
因為只有5這個數字 ，所以只會跑一次，時間複雜度是O(n)

如果我們用一般的quick sort ，就算一直取5的中間 ，最快也只有O(nlogn)

75. Sort Colors 就是Dutch National Flag Algorithm

quicksort 好像也有stable的版本 。之後再了解