堆積(Heap)

堆積，是一種樹狀結構，用於實現「優先佇列(Priority queue)」。Priority queue是資料結構的一種，可以自由追加數據，讀取資料時，從最小值開始選取。
堆積是一種完整的二元樹，儲存在一維陣列內，分成MaxHeap及MinHeap。

• MaxHeap：上一層的節點數值>=下一層的所有節點
• MinHeap：上一層的節點數值<=下一層的所有節點

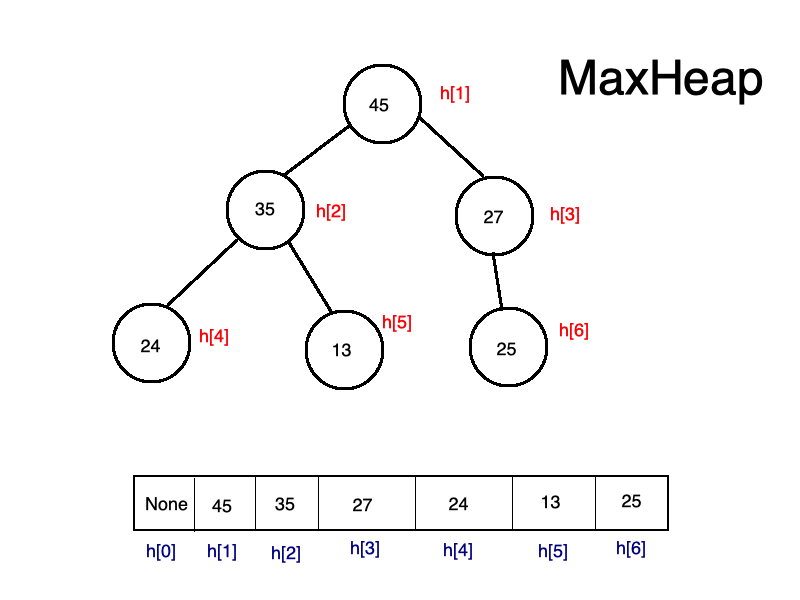
建立Heap步驟如下：

1. 先將一維陣列轉換為Heap結構
   • 由小到大排序：使用MaxHeap
   • 由大到小排序：使用MinHeap
2. 從堆積結構依序取出Root，與最後一的元素交換，再將除了最後一個節點外的一維陣列轉換成堆積結構，重複執行直到剩下最後一個元素，排序完成。

堆積排序(Heap Sort)

• 堆積排序最初要將n個數儲存到堆積中的時間是O(n log(n))。
• 此外，每回合取出最大值，再重新排列堆積，所需時間是O(log n)，回合數是n，堆積重整後接著排序的執行時間也是O(n log(n))，由此得知，堆積排序的整體執行時間是O(n log(n))。
• 與氣泡排序、選擇排序、插入結構相比，堆積排序處理速度較快，但也因為這種複雜的資料結構，建置與維護變得複雜。

import random

#從1-100中隨機讀取8個數字
nums = random.sample(range(1,100), 9)
print(nums)

def max_heapify(h, n, x):
    #如果(2*x+1) <= n，表示有右子節點
    if (2*x+1) <= n :
        #如果h[2*x] > h[2*x+1]，表示左子節點大於右子節點
        if h[2*x] > h[2*x+1]:
            max = 2*x
        else:
            max = 2*x+1
    else:
        max = 2*x
    #如果h[x]<h[max]，則兩個子節點互換
    if h[x] < h[max]:
        h[x], h[max] = h[max], h[x]
        #如果2*max<=n，表示h[max]也有子節點，recursion max_heapify是否與孫節點互換
        if 2*max <= n:
            max_heapify(h, n, max)

#將任何陣列轉換為Max Heap
def build_max_heap(h, n):
    #迴圈變數
    for i in range(n//2, 0, -1):
        max_heapify(h, n, i)

def heap_sort(h, n):
    build_max_heap(h, len(h)-1)
    print(h)
    for i in range(n, 1, -1):
        h[i], h[1] = h[1], h[i]
        if i > 2:
            max_heapify(h, i-1, 1)
        print(h)

heap_sort(nums, len(nums)-1)
print(nums)

let heapSize;
let arr = [15, 3, 17, 18, 20, 2, 1, 666];
heapSort();
console.log(arr);

function buildMaxHeap() {
  heapSize = arr.length - 1;
  for (let i = Math.floor(heapSize / 2); i >= 0; i--) {
    maxHeapify(i);
  }
}

function maxHeapify(i) {
  let largest;
  let l = i * 2 + 1;
  let r = i * 2 + 2;
  if (l <= heapSize && arr[l] > arr[i]) {
    largest = l;
  } else {
    largest = i;
  }

  if (r <= heapSize && arr[r] > arr[largest]) {
    largest = r;
  }

  if (largest != i) {
    // swap A[i] with A[largest]
    let temp = arr[i];
    arr[i] = arr[largest];
    arr[largest] = temp;
    maxHeapify(largest);
  }
}

function heapSort() {
  buildMaxHeap();
  for (let i = arr.length - 1; i >= 0; i--) {
    // exchange A[0] with A[i]
    let temp = arr[0];
    arr[0] = arr[i];
    arr[i] = temp;
    heapSize -= 1;
    maxHeapify(0);
  }

  return arr;
}

結論

排序演算法到今天告一個段落，明天要開始新的演算法，下表整理了這幾天的排序演算法：

後續會再繼續補充資料，目前先這樣吧！