使用字典建立圖形資料結構

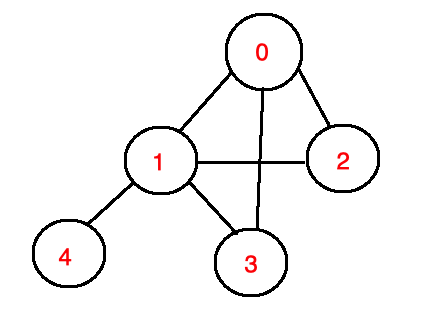
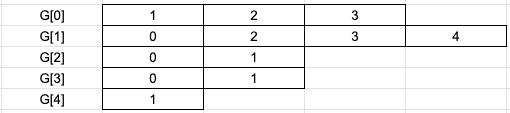
字典鍵值對應串列如下，配合圖表更容易理解。

• G[0]:[1,2,3]
• G[1]:[0,2,3,4]
• G[2]:[0,1]
• G[3]:[0,1]
• G[4]:[1]

import sys

#使用字典建立Graph
G={}
#不斷輸入一個數字到變數line
for line in sys.stdin:
    #將變數line轉換成整數儲存到變數n，表示有幾個邊要輸入
    n = int(line)
    #使用迴圈變數i，從0到n-1，每次遞增1，迴圈執行n次
    for i in range(n):
        #每次輸入兩個整數到變數a跟b，表示邊的兩個頂點
        a, b =input().split()
        a = int(a)
        b = int(b)
        # a在字典G內
        # 如果字典G包含鍵值a，則將b加入到G[a]的最後，表示點a可以到點b
        if a in G.keys():
            G[a].append(b)
        # 否則建立新的鍵值a對應到串列，該串列有一個元素b
        else:
            G[a]=[b]
        # 如果字典G包含鍵值b，將a加入到G[b]的最後，表示點b可以到點a
        if b in G.keys():
            G[b].append(a)
        # 否則建立新的鍵值b對應到串列，該串列有一個元素a，表示點b可以到點a
        else:
            G[b]=[a]

程式碼參考資料：資料結構使用Python

深度優先搜尋(Depth-First Search(DFS))

深度優先搜尋具有深入單一路徑往下探查的特徵，廣度優先搜尋和深度優先搜尋的搜尋順序大不相同，但過程的差異只有一個，也就是要從選項的頂點中選擇哪個點。

頂點選項：「後進先出」(LIFO)的方式管理，可以用「堆疊」的資料結構

廣度優先搜尋是選擇最早被加入選項的頂點，因為先從距離起點較近的頂點開始搜尋，所以會從起點附近依序探查。
深度優先搜尋是選擇最晚被加入的頂點，所以並不折返，而是一直深入新開發的路徑

使用DFS找最長路徑長度

# 使用字典將節點名稱轉換為節點編號，將邊的節點編號加入圖形資料結構中，以字典表示，最後使用DFS，找出最長邊的個數

G = {}
City = {}
# 宣告陣列v為一維整數陣列，有210個元素，每個元素初始化為0
v = [0]*210
# 初始化md為0
md = 0
# 將節點名稱轉換為數字，使用字串p為輸入，將節點名稱p轉換為節點編號
def getCityIndex(p):
    if p not in City.keys():
        City[p].len(City)
    return City[p]

# DFS找尋最深的深度
def DFS(x,level):
    # 存取第4行全域變數
    global md 
    # 使用迴圈讀取節點編號x的所有邊可以連結出去的節點，迴圈變數i由0到G[x]的長度減1
    for i in range(len(G[x])):
        # 若level > md，則md = level，md為最長路徑邊數
        if level > md:
            md = level
        # 設定變數target為G[x][i]，G[x][i]表示讀取G[x]的第i個元素
        target = G[x][i]
        # 變數target設定為能由節點編號x連結出去的節點G[x][i]
        # 若v[target]等於1，表示已拜訪過，使用continue跳到迴圈開頭
        if v[target] == 1:
            continue
        v[target] = 1
        DFS(target,level+1)
# m = 輸入邊的個數到
m = int(input())

# 迴圈跑m次，每次輸入兩個節點a和b
for i in range(m):
    a, b = input().split()
    a = getCityIndex(a)
    b = getCityIndex(b)
    # a在字典G內
    # 如果字典G包含鍵值a，則將b加入到G[a]的最後，表示點a可以到點b
    if a in G.keys():
        G[a].append(b)
    else:
        G[a] = [b]
    # b在字典G內
    if b in G.keys():
        G[b].append(a)
    else:
        G[b] = [a]

# 輸入字串到字典City查詢節點編號
start = City[input()]
#使用DFS走訪，輸入start與0，表示從start開始，且階層開始為0
DFS(start, 0)
print(md)

程式碼參考資料：資料結構使用Python