前言

前一天提到的Hybrid Cryptosystem，其中使用到的「key」會進行封裝，避免被有心人士擷取將加密後的訊息解密。其中用得到的方法就是今天會提到的迪菲-赫爾曼金鑰交換(Diffie-Hellman Key Exchange)。

迪菲-赫爾曼金鑰交換(Diffie-Hellman Key Exchange)

名稱雖然為Key Exchange，但意思是產生金鑰。

迪菲-赫爾曼金鑰交換是在兩方之間安全交換金鑰的方法，「混合運算」雙方共享的秘密數和公開數後，就能安全地交換雙方的共同金鑰。方法是用質數P、生成元G、和G的x次方mod P來求出X的問題，稱為「離散對數問題」(discrete logarithm problem)，目前尚未找到有效率的解法。

不過我們先來看看Diffie-Hellman的運算方式：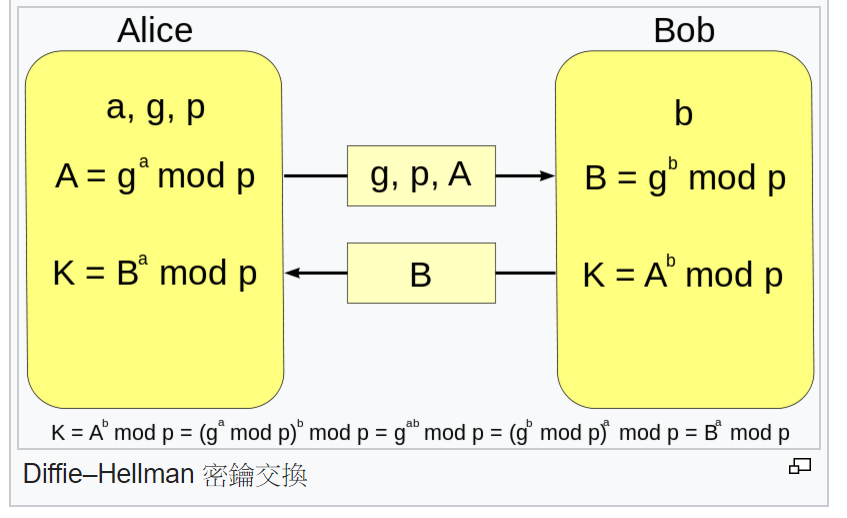

資料來源：Wiki

使用Python實現Diffie-Hellman Key Exchange

class DH_Endpoint(object):
    def __init__(self, public_key1, public_key2, private_key):
        self.public_key1 = public_key1
        self.public_key2 = public_key2
        self.private_key = private_key
        self.full_key = None
       
    def generate_partial_key(self):
        partial_key = self.public_key1**self.private_key
        partial_key = partial_key%self.public_key2
        return partial_key
    
    def generate_full_key(self, partial_key_r):
        full_key = partial_key_r**self.private_key
        full_key = full_key%self.public_key2
        self.full_key = full_key
        return full_key
    
    def encrypt_message(self, message):
        encrypted_message = ""
        key = self.full_key
        for c in message:
            encrypted_message += chr(ord(c)+key)
        return encrypted_message
    
    def decrypt_message(self, encrypted_message):
        decrypted_message = ""
        key = self.full_key
        for c in encrypted_message:
            decrypted_message += chr(ord(c)-key)
        return decrypted_message
        
        
        
message="This is a very secret message!!!"
s_public=197
s_private=199
m_public=151
m_private=157
Sadat = DH_Endpoint(s_public, m_public, s_private)
Michael = DH_Endpoint(s_public, m_public, m_private)

參考資料：Diffie-Hellman Key Exchange explained (Python)