前言

走過了資料分析、演算法選擇後，
我們得知了有些可以改善模型的方向:

1. 解決資料不平衡(Done)
2. 學習率的設定(Now)
3. 訓練輪數(To do)
4. 模型深度(No, I want my model to be more efficient ! )
5. 階段式訓練(To do)

林俊傑唱過：

總是學不會　再聰明一點

眾所周知，最佳化就是在調整模型參數以降低loss值，
而這個調整的速度會被學習速率(learning rate)控制，
learning rate越大就會改變參數越多。
optimizer如SGD、ADAM都會根據導數乘以learning rate來改變參數值。
所以 learning rate在訓練模型時非常重要。
也會讓網路更聰明地學習！

學習率衰減

學習率衰減是訓練模型的小技巧，
通常我們會希望學習率一開始大，
這樣才會學得快(損失函數收斂速度快)。
但隨著訓練時間提升，
模型參數已經趨於穩定，
我們會希望學習率減小，
才會穩穩地在global minimum來回。
(local minimum 你走開= =)

1. step decay

每隔n輪依比例下降。

學習率圖形: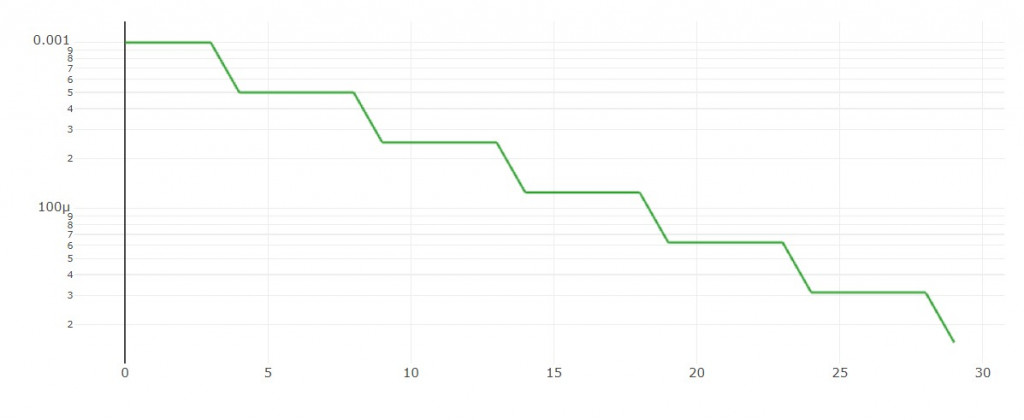

程式碼實作:

def step_decay(epoch):
    """
    Warm-up applying high learning rate at first few epochs.
    Step decay schedule drops the learning rate by a factor every few epochs.
    """
    lr_init = 0.001
    drop = 0.5
    epochs_drop = 5
    warm_up_epoch = 0
    if epoch+1 < warm_up_epoch:  # warm_up_epoch之前採用warmup
        lr = drop * ((epoch+1) / warm_up_epoch)
    else:  # 每epochs_drop個epoch，lr乘以drop倍。
        lr = lr_init * (drop**(int(((1+epoch)/epochs_drop))))
    return float(lr)

甚麼是warm-up?

大家可能注意到我有設一個參數是warm_up_epoch，
如果這個warm-up等於5，
代表前5輪訓練時我使用由小漸大的學習率，隨後使用step-decay。
例如: 0.0001, 0.0003, 0.0005, 0.0007, 0.0009, 0.001, 0.0005, 0.000025, ...
有人相信這個方法可以讓模型後續收斂得更穩定。
(但我在這次實驗中沒有用到這個機制)
請參考這篇文章。

2. exponantial decay

每隔1輪依照指數下降
學習率圖形: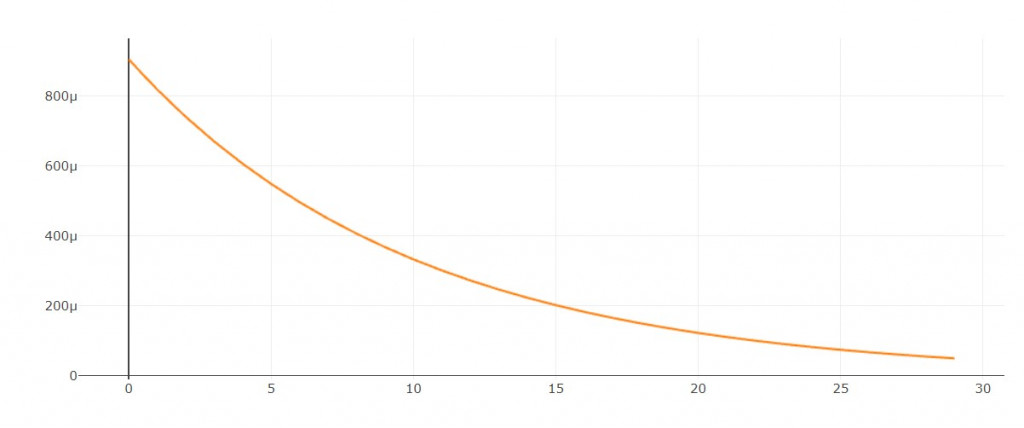

程式碼實作:

def exp_decay(epoch):
    lr_init = 0.001
    lr = lr_init * tf.math.exp(-0.2 * (epoch+1))
    return float(lr)

3. polynomial decay

每隔1輪依照多項式函數下降
這裡我加上一個循環機制

    if global_step >= decay_steps:
        global_step = global_step % decay_steps

使得每隔n輪會重複相同圖形
用意是: 當我陷入區域最小值的泥沼時，有機會跳出來。
學習率圖形: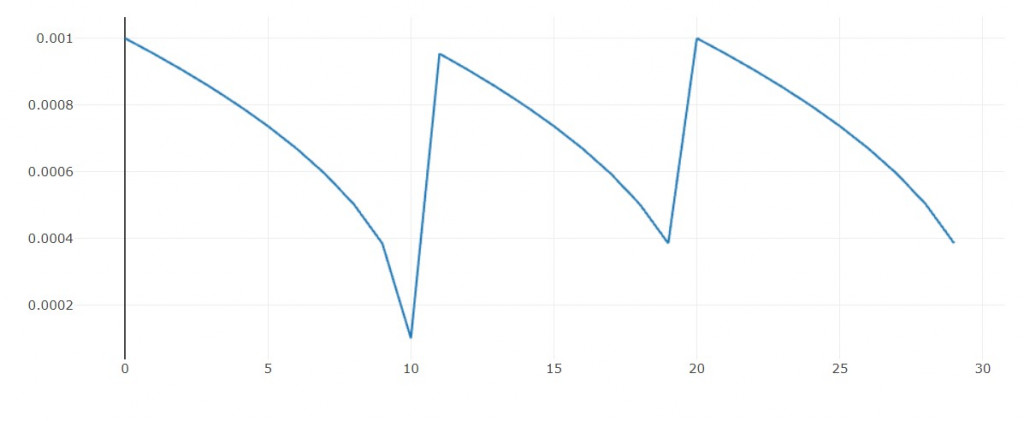

程式碼實作:

def poly_decay(epoch):
    lr_init = 0.001
    lr_end = 0.00001
    decay_steps = 10
    global_step = epoch
    power = 0.5
    if global_step >= decay_steps:
        global_step = global_step % decay_steps

    lr = (lr_init-lr_end)*((1-(global_step/decay_steps))**power) + lr_end
    return float(lr)

實驗結果

• 這裡要注意，因為EFN_poly從第11輪開始有循環，所以我們比較第10輪的表現。

驗證準確率:step>poly>exp(準確率越大越好) in 10th epoch

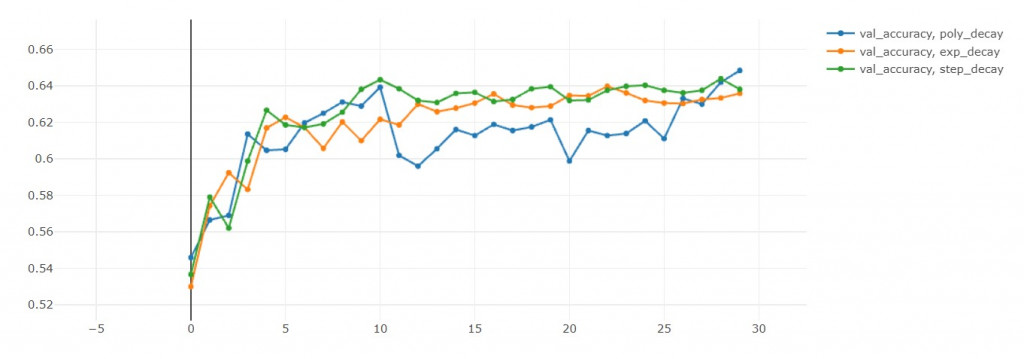
驗證損失值:exp<poly<step(損失值越小越好) in 10th epoch

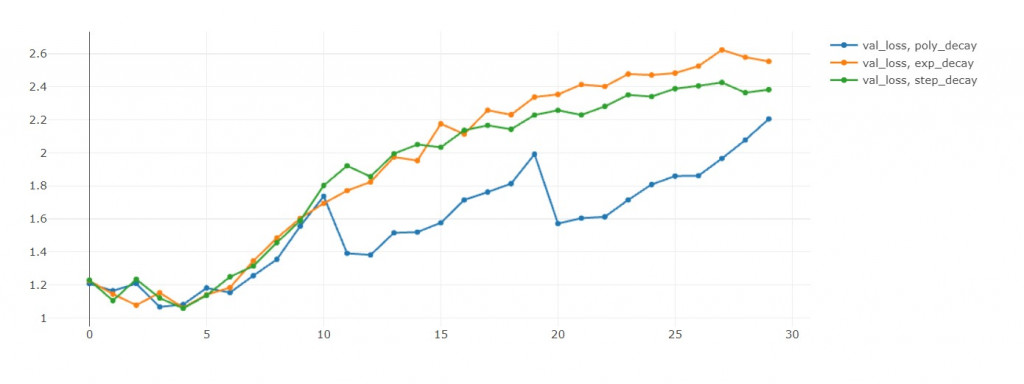
訓練準確率:poly>step>exp in 10th epoch

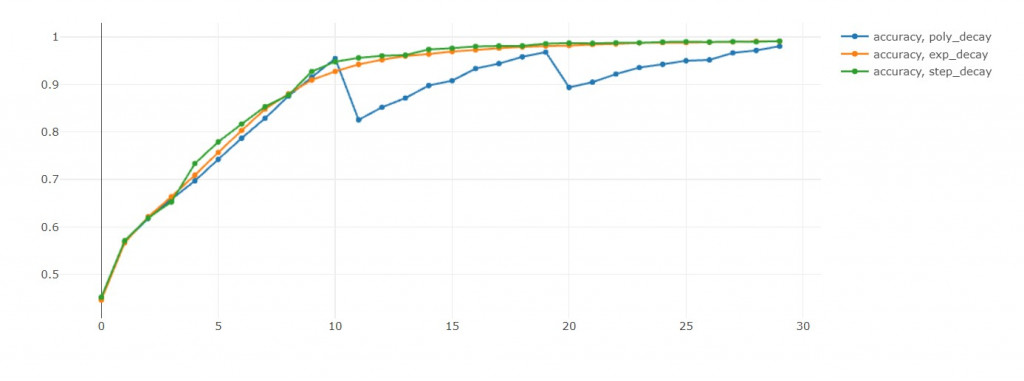
這裡蠻有趣的地方是poly的循環機制，
可以從驗證準確率和驗證損失值中發現，
每次學習率回到初始值，這兩者都會往下掉。
損失值下降是我們樂見的，代表演算法跳出之前的區域最小值，
前往尋找另一個區域最小值。
當然我不用擔心演算法找不到另外一個區域最小值，
因為我可以儲存每個epoch的模型。
但如果沒有循環機制，
我就要擔心演算法困在這一個區域最小值了！

comparing all metrics

模型 | 訓練時長(秒) | acc | loss | val_acc | val_loss
------------- | ------------- | ------------- | -------------
EFN_step | 1960 | 0.991(勝) | 0.026(勝) | 0.638 | 2.383
EFN_exp | 2083 | 0.991 | 0.029 | 0.636 | 2.554
EFN_poly_cyclic | 2018 | 0.98 | 0.057 | 0.648(勝) | 2.205
EFN_base | 2004 | 0.952 | 0.139 | 0.617 | 1.905(勝)

結語

1. exp dacay的學習率下降太快，導致模型還沒在這個學習率上好好最佳化就縮小學習率了。
2. step dacay應該是比較理想的方法，能夠學得充分，不像其他兩個方法每輪都下降。
3. 循環機制很棒，以後要試試搭配其他衰減法。