9.2 找出分離點對 (Separating Pair)

如果一個點的子集合移除以後，會讓圖 G 變得不連通，那麼這個集合被稱為分離集 separting set (又被稱為 vertex cut)。如果這個集合只包含兩個點，那我們便稱它為分離點對 separating pair。顯然一個圖 G 如果是三連通，若且唯若圖 G 不包含任何的分離點對。

今天我們來聊聊找出分離點對的 Hopcroft-Tarjan 演算法 (https://epubs.siam.org/doi/abs/10.1137/0202012 Section 3) 。
這篇文章所提及的演算法其實有一個很微妙的小錯誤，由 Gutwenger 與 Mutzel 等人在 2001 年提出校正。(可以參考他們的論文 https://link.springer.com/content/pdf/10.1007/3-540-44541-2_8.pdf )
這個 Hopcroft-Tarjan 演算法可以找出所有的分離點對(但不一定列出他們，畢竟如果輸入是一個圈的話，可能會有 N^2 個分離點對)，我們今天先討論出怎麼找出一個分離點對就好。只要確定有、或沒有，就能夠判斷這張圖是否為三連通的了。

首先，我們可以假設整張圖已經是雙連通的了：只要先跑過一次找關節點的 DFS 就可以。現在，讓我們來想一下，如果有兩個點形成 separation pair，那麼他們在 DFS樹(這類型沒有 cross edge 的搜索樹又可以被類似地定義為棕櫚樹 palm tree) 上會長什麼樣子。在找關節點的過程中，我們會順便計算 lowpt(x)：從 x 出發往下走若干路以後沿著回溯邊，看看最淺可以回到深度多少的祖先。在找分離點對的時候，可能這個祖先會被暫時移除，此時就必須要考慮第二淺的祖先了。於是我們定義了 lowpt2(x)，代表從 x 往下走若干路以後沿著回溯邊，能會到的第二淺祖先的深度。

有了 lowpt(x) 和 lowpt2(x) 這兩個數值以後，就可以把整棵DFS樹(以及回溯邊) 按照一個特定的方式編號，根據下面所述的性質，從而找出分離點對。

如果 {a, b} 是一組分離點對(且 a 在樹上編號比 b 小，這意味著 a 是 b 的祖先)，那麼若且唯若它們是以下幾種之一：

• 第一型分離點對：存在另外兩個點 r, s，使得 r 是 b 的孩子、lowpt(r) = a、lowpt2(r) >= b 並且 s 既不是 r 的後代也不是 a 更不是 b。這麼一來把 a, b 拿走的時候 r 所在的子樹會斷開，與 s 不連通。
• 第二型分離點對：存在 r 是 a-->b 這條路上的第一個點(a 的孩子)，滿足編號 r 到 b 之間的節點，其回溯邊 (x, y) 都有 y 編號比 a 大(也就是越不過 a)、此外也滿足 b 的所有子孫，若有人回溯到 a 與 b 之間的話必須要 lowpt(w) >= a，其中 w 是 b 往該子孫方向走遇到的第一個節點(這句話是說，如果所有回溯邊都越過 a 那就越過吧毫不在意)。

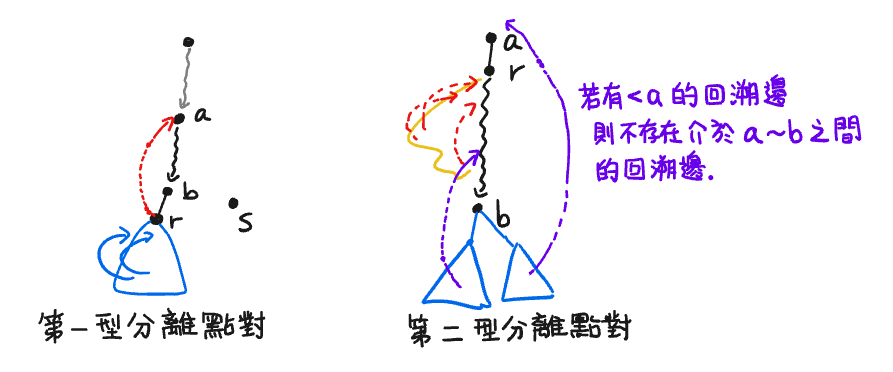
根據上述這兩個條件以及 "特定的方式編號"，就能設計出線性時間的演算法啦。
至於 "特定的方式編號" 是什麼呢，其實就是依照 lowpt2(w) 的值對所有 v 的鄰邊 (v, w) 進行排序啦，其實很短但是因為這邊沒有證明所以寫下來也沒太多意義。詳情可以參考 Gutwenger-Mutzel 的論文第 4.2 節中間的 phi 函數。

9.X 冷笑話

為什麼學習圖論的時候都會遇到樹呢？因為不學無樹啊。