9.3 三連通元件

3連通跟2連通真的不太一樣。
以2連通來說，如果我們今天把整張圖，依照關節點切開，形成很多破碎子圖(也就是允許有某些邊懸掛在圖上，其中一個端點並不在子圖的點集內，這張子圖不算是一個圖)，此時我們可以說對於每一個不完整的圖內部的任何兩個點，都能夠透過兩條點不重複的路徑相連，而且這兩條路徑都在該破碎子圖內部。此外，若兩個點分屬不同的破碎子圖的話，那麼他們之間一定不存在兩條點不重複的路徑。

但是同樣的定義套用在3連通元件卻說不通。考慮下面這張圖：我們知道 u 和 v 之間有3條點不重複的路徑聯絡彼此，但是將 {u, v} 這兩個點拿掉以後，會拆出三個破碎子圖。考慮其中一個破碎子圖，若我們挑選兩個點，它雖然在原本的圖上存在 3 條點不重複的路徑，但是其中會有一條繞出破碎子圖。也就是說我們在考慮把這些邊劃分出去的時候，還得考慮 3條路徑有一條繞出去的情形...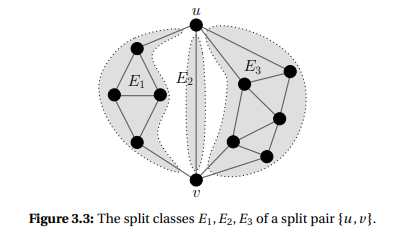

(圖片來源：https://d-nb.info/1010461893/34)

這個現象最早由美國數學家 MacLaine 於 1937 年率先提出。然後在 1966 年由任職於多倫多大學的英國數學家 Tutte 引進了 "虛擬邊" 的概念，將 3連通圖的理論更完整地刻畫出來。有了這些圖結構的刻畫以後，接下來就是設計演算法的部分了。除了 1973 年發表的 Hopcroft-Tarjan 演算法以外，在 1989 年由兩位義大利人 Di Battista (現在任職於羅馬大學) 以及 Tamassia (現在任職於布朗大學) 提出了一個叫做 SPQR-樹的資料結構，這讓動態處理 3連通元件變得相當有效率。