上一回寫到樹，今天的主題是以樹結構為基礎的資料結構。

堆積

二元樹(binary tree)是每個節點最多只有兩個子節點的樹結構，而其中完全二元樹(complete binary tree)是指除了最後一層有可能沒有填滿外，其餘中間每一層的滿節點的二元樹，也就是一個節點都一定有兩個子節點。最後一層如果是不滿的情況，則節點都會在該層的左側。

堆積就是一種特別的完全二元樹，它的任一節點的值會比其子節點的值小(或大)。如果任一節點比子節點小，稱為最小堆積(min heap, 如下圖左)；任一節點比子節點大，則稱為最大堆積(max heap, 如下圖右)。

圖片來源：GeeksforGeeks

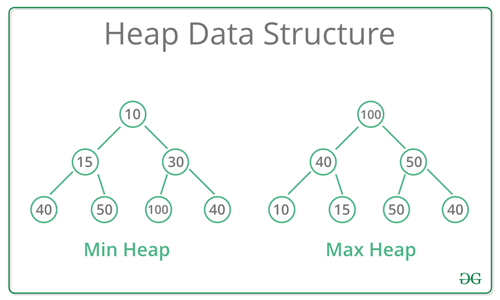
堆積的結構讓存取最大或最小元素只需要O(1)，可以應用來提升很多演算法的效率。其中一個很常與堆積一起提到的演算法就是堆積排序(heapsort)。

以由大到小的排序來說，堆積排序的作法是先將要排序的元素組成一個堆積，接著反覆將最大的節點移除，同時維持剩下的節點為堆積的結構，直到只剩一個節點，則排序結束。堆積排序可以說是選擇排序的進化版，它也是逐一將最大的元素排序進陣列中，不過因為資料結構確保了最大元素的存取，就省去了每一輪比較所有元素的操作。最壞情況執行時間為O(n log n)。

字首樹

trie(音'try')，又稱作字首樹(prefixed tree)，是一種搜尋樹的資料結構，通常用來儲存比較複雜的資料，如字串。它與二分搜尋樹不同的地方在於，二分搜尋樹會在一個節點上儲存整個資料(一個字串)；字首樹的一個節點上則只儲存字串中著一個字元(character)。透過搜尋一個節點的所有子節點可以存取字串。

以下圖來說，從根節點開始，可以透過相連的節點搜尋到geer這個字串，而第二個e以下任何子節點組成的字串也都會共用gee這個字首，例如geeks。

圖片來源：GeeksforGeeks

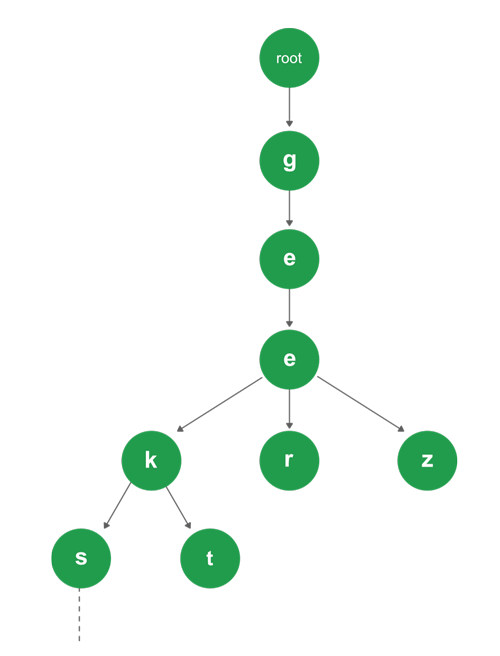
實作上，字首樹可以是以陣列作為節點的樹，陣列均由字母組成。以儲存的一個字串來說，字串的第一個字母會指向一個陣列，陣列中的下個字母會再指向一個陣列...直到最後一個字母以布林值表達字串結束。若搜尋時碰到一個陣列中沒有下一個陣列的參照或布林值，則代表的找想的字不在樹中。

在字首樹中搜尋任一長度為m個字元的字串，只要經過m個步驟。而且m不會因為樹中的總字串數(n)增加而改變，也就是可以實現O(1)的搜尋，相較之下比二分搜尋樹的O(log n)還快。不過搜尋速度這麼快的同時，可以想像字首樹的空間需求非常高。