樹有非常多變型，下面是Wiki的截圖

以下簡單介紹幾種常聽到的～

AVL Trees、Red Black Trees

前幾篇介紹的是最基本的二元樹，但實際上不太會直接用到二元樹，因為它不會做平衡，如果一直對它做insert，很容易就會歪一邊，大大影響效能。之前有提到的兩種比較常聽到的平衡樹，AVL Trees 和 Red Black Trees。
平衡樹在做insert的時候，會做旋轉操作(左旋，右旋等)，根據值去調動節點的位置，讓整個樹一直保持在平衡的狀態。
一般來說Red Black Trees在insert&delete上比AVL樹有優勢，AVL樹則在serach有優勢。

兩種樹的程式都很複雜，因為在插入跟刪除的時候，都有很多case要處理，大家有興趣可以再去研究
不過一般來說，我們有需要都會去github找package來用XD，很少情境要你去刻一個出來

B+ Tree

這一種就是MySQL InnoDB底層的資料結構
平衡二元樹在搜尋的速度上的確很優秀，但不好去讀取大量的資料，如果我們要去找id 1到20的資料，那就要搜尋20次。其次二元樹每一個節點底下只可以有兩個子節點，DB資料隨便都幾百萬千萬，這顆樹的深度就很可怕了，這也會影響到搜尋的速度。

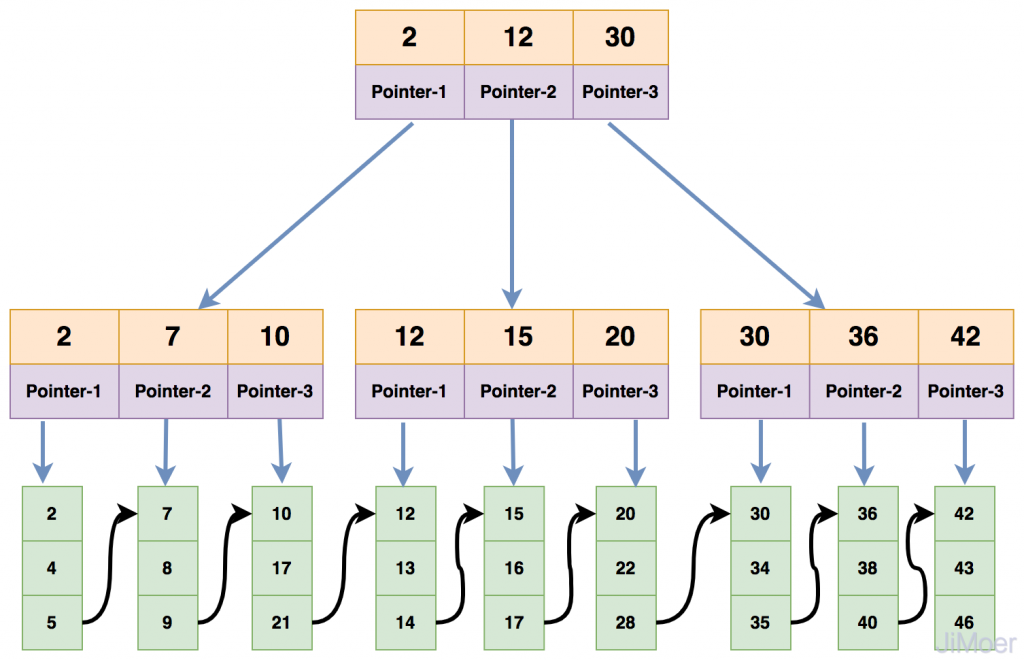
而B+ Tree就解決了這些問題
最下面綠色的是真正的資料，以MySQL來說是一頁，頁跟頁之間有做鏈結，每一頁都有下一頁的地址。以B+Tree來搜尋id 1到20的資料，我們就可以透過樹來找到id 1的頁在那，再從頁裡面照順序找1~20的資料，就可以一次回傳！樹就是一個索引的概念，讓我們可以快速找到頁的位置～

圖源在這一篇文章找的，內文寫得很細，大家有興趣可以看看～

Binary Heap

中文叫二元堆積，是為了解決Priority Queue的一種方式
那什麼是Priority Queue？
簡單來說在隊列裡面加入權重，舉個例假如一堆平民先進去排隊，但權貴人土可以隨時插隊的概念(像打疫苗)，又或者是待辦清單，原本就照重要的程度去做排序，但突然有一個緊急的事情，就會插到清單最前面。

Min Heap (root為最小值)

            1         
         /      \        
       2         3                      
    /    \     /   \                 
   4      5   6     7               
  / \    / \                      
 8  9   10 11                     

Max Heap (root為最大值)

          11 
       /      \ 
     9         10
   /   \     /    \ 
  5      6   7      8
 / \    / \
1   2  3   4 

再做Heap sort就可以做出Priority Queue的效果，大家有興趣再去研究～

今天先到這樣～Bye