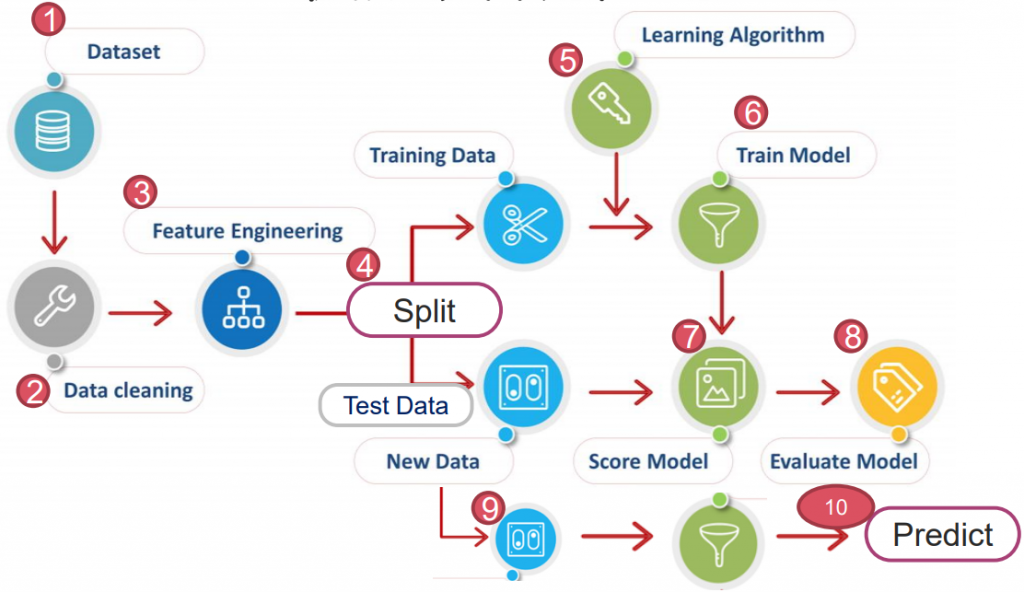
https://yourfreetemplates.com/free-machine-learning-diagram/
本篇會著重在先前提過的監督式學習上。
依據資料類型不同,監督式學習又分以下兩種:
資料集以"有限的類別"分布,對於其做歸類,即分類。
資料集以"連續的方式分布",對於其以線性方式描述,即迴歸。
概念是由 Michael Kearns 提出,指一個訓練模型結果只比隨機分類好一點的演算法,稱弱學習器。
反之,強學習器則是指經演算法訓練後,模型預測結果非常接近真實情況。
以下會以 breast_cancer(Classification)資料來介紹常見的弱學習器:
import pandas as pd
from sklearn import datasets
ds = datasets.load_breast_cancer()
X=pd.DataFrame(ds.data, columns=ds.feature_names)
y=pd.DataFrame(ds.target, columns=['Cancer'])
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3)
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train_std = sc.fit_transform(X_train)
X_test_std = sc.fit_transform(X_test)
尋找距離預測值最近的 N 個樣本點,以多數決(Majority Voting)決定所屬分類。
優點:實現只須兩個參數 P & 距離函數。
缺點:無法應用於高維度,且不適用類別(定性)特徵(如性別、星期幾...等非數字資料)。
常用於推薦商品。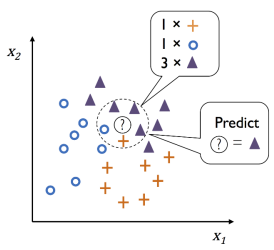
from sklearn.neighbors import KNeighborsClassifier as knn
clf = KNN(n_neighbors = 3)
clf.fit(X_train_std, y_train)
clf.score(X_test, y_test)
>> 0.9707602339181286
超參數:
1. n_neighbors: 預測值須取多少臨近點比較。為避免平局常取奇數。
2. metric: 計算距離的公式。
其為線性迴歸的改良版。(數學原理可參考:推導1、推導2 & 推導3)
優點:Outlier 影響小(上下限 0~1),可線性分割。平滑曲線,變異性小。
缺點:無法應用於高維度、易未擬合,且對於非線性特徵要額外轉換。
常用於二分類。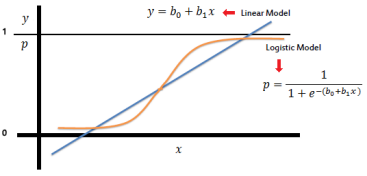
from sklearn.linear_model import LogisticRegression as LR
clf = LR(penalty='l2', C=0.01)
clf.fit(X_train_std, y_train)
clf.score(X_test_std, y_test)
>> 0.9649122807017544
超參數:
1. penalty: 正則化參數。預設 l2。(詳細解說)
L1: 將沒有用的權重設為0,留下模型認為重要的權重
L2: 削弱所有權重(但仍保留),讓所有權重與神經元都處於活動狀態。
2. C: 正則化強度的倒數。C 越小,矯正強度越大(使訓練分數降低、預測資料變準)。
如圖,距離 model(方程式)最近的點,稱為 Support Vector 支援向量,
而 positive Hyperplane & negative Hyperplane 彼此間距為 margin。
其根本目的為找到一個 Decision Boundary,使切割的 margin 越大越好。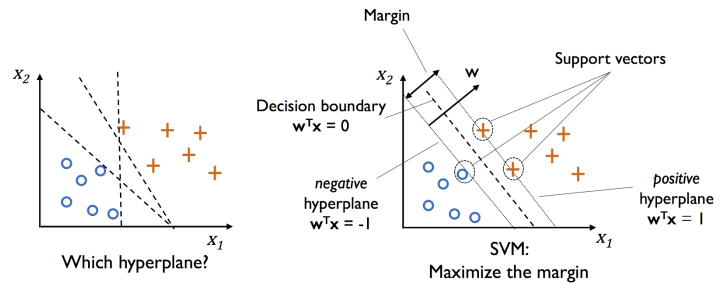
優點:Outlier 影響小(僅邊界影響),且記憶體用量小。高維資料表現好。多樣核函數以應對資料。
缺點:樣本數大時效能差(須來回優化),成本貴。
from sklearn.svm import SVC
clf = SVC(C=1, probability=True)
clf.fit(X_train_std, y_train)
clf.score(X_test_std, y_test)
>> 0.9649122807017544
可以查看其參照多少支援向量:
len(clf.support_vectors_)
>> 97
超參數:
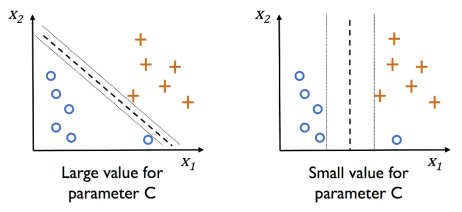
1. C: 正則化強度的倒數。C 越小,矯正強度越大(使訓練分數降低、預測資料變準)。
默認 1(hard margin,盡可能找出完美超平面,下圖左)。
若 C=0.01,則模型評分會下降至 0.66。
2. kernel: 同 PCA,有 {‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’} 等分類方式。
若使用 'linear' 分析圓形資料,評分會下降許多
3. probability: True 才能使用 predict_proba 呼叫機率。
PS. 此外,sklearn 有提供三種線性分類寫法:
# 1. 較常使用
LinearSVC(C=1, loss='hinge')
# 2. 執行效能較差
SVC(kernal='linear', C=1)
# 3. 適合記憶體有限(訓練資料很龐大) or Online Training
SGDClassifier(loss='hinge', alpha=1/(m*C))
透過 training data 的 fearture 學出一系列的問題,然後來推斷其分類。
演算法
A. Sklearn 使用的是 Classification and Regression Tree (CART)
特色為依照數值型特徵切割,且一次切割只分為兩個點,但同一特徵可多次切割。
B. Chi-squared Automatic Interaction Detection (CHAID)
所有變數轉成不連續的組距(discretecized),切割可大於兩個點。
C. 其他還有 ID3、ID4.5、ID5.0、Decision Stump、M5...等。
Information gain 信息增益
為了能在節點上使用最具意義的特徵來分割,我們會透過信息增益來判斷。
信息增益越大,那此「分類」對於決策樹來說就越重要,表示它能把數據分的越乾淨。
所謂的信息增益,可用以下方式表達:
常見信息增益計算:
A. Gini Impurity 吉尼不純度:
計算一「隨機樣本」被某個「分類 x 」分錯的概率。不純度越低,表示該分類方法越顯著有用。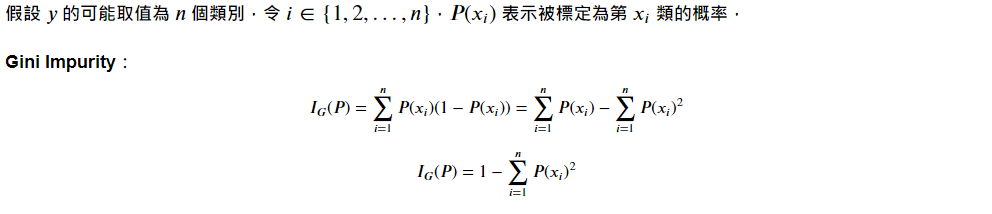
Ex. 假設分類後僅剩下 1 種特徵,則 Ig = 1-(1+0) = 0,為一個不純度最低的完美分類方法。
(多考慮純度,故比起 Entropy,分類效果較好)
B. Entropy 熵:
類似熱力學,但在資訊理論中多了負號。熵高(負少)傳輸資訊多,熵低(負多)則傳輸資訊少。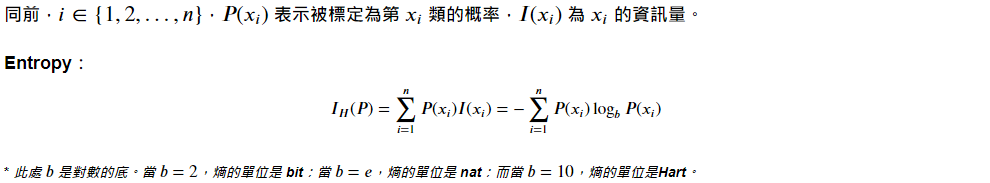
C. Classification Error 分類錯誤率:
很直觀,即分類錯誤的最小機率。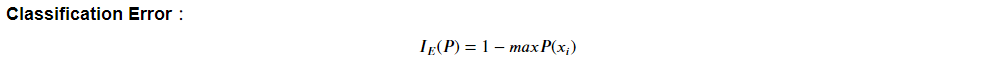
優點:易於瞭解與解釋(可視覺化)。資料僅須少量前處理(不需常態/標準化)。無複雜計算。
缺點:易過擬合,需搭配特徵選擇減少特徵量。不平衡樣本(得病/無病)差距太多,會使分割偏向多數樣本方,需使用 class balancing 技術(如 SMOTE)矯正。
程式碼
*注意!!! 決策樹演算不需要標準化/正則化的!!!
它們不關心特徵「值」,只關心特徵「分佈」和特徵間的「條件概率」
import pandas as pd
from sklearn import datasets
ds = datasets.load_breast_cancer()
X=pd.DataFrame(ds.data, columns=ds.feature_names)
y=pd.DataFrame(ds.target, columns=['Cancer'])
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3)
決策樹:
from sklearn.tree import DecisionTreeClassifier as DTC
clf = DTC(criterion='gini', max_depth=3, random_state=1)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
>> 0.9064327485380117
超參數:
1. criterion: 不純度方法,'gini'(默認) & 'entropy'。
2. max_depth: 樹的層數。若 None 則擴展節點至所有葉包含 min_samples_split 樣本。默認 None。
3. min_samples_split: 分裂一個內部節點所需的最小樣本數。默認 2。
更多參數看 DecisionTreeClassifier或 DecisionTreeRegressor
要讓決策樹視覺化,需安裝以下兩個程式:
Graphviz (官方網站)
下載後,進入主機(右鍵)內容 -> 進階系統設定 -> 環境變數 -> Path
並新增"C:\Users\User.conda\envs\tensorflow-gpu\Lib\site-packages\graphviz\bin"
使用 pip 安裝 pydotplus
pip install pydotplus
正式使用:
# 作圖
from pydotplus import graph_from_dot_data
from sklearn.tree import export_graphviz
dot_data = export_graphviz(clf,
filled = True,
class_names = ds.target_names,
feature_names = ds.feature_names,
out_file = None)
graph = graph_from_dot_data(dot_data)
graph.write_png('Pic\Cancer tree.png')
# 顯示圖片
from IPython.display import Image
Image(filename='Pic\Cancer tree.png', width=1000)
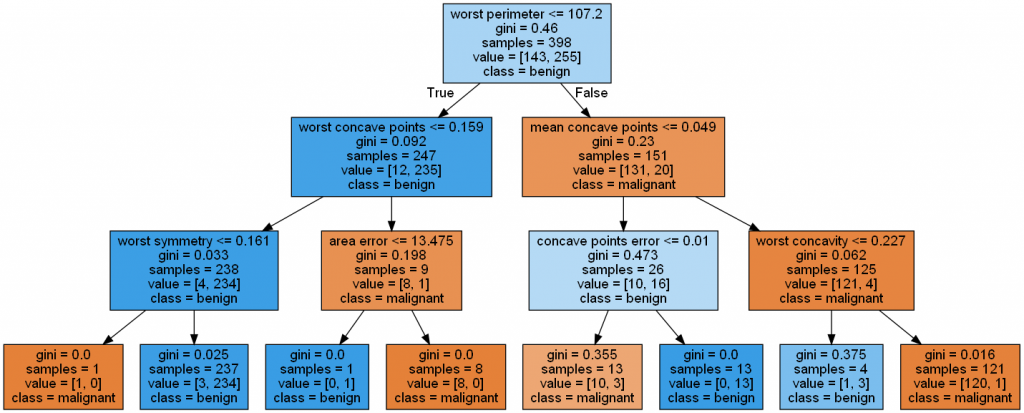
另外,Decision Tree 也可以應用於迴歸類型的資料,見補充 4.。
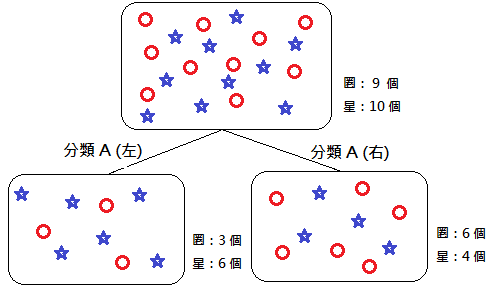

*補充 2.:Entropy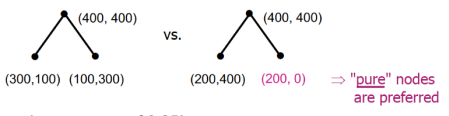
左右兩邊的 Etropy 算出來皆為 0.5,但
*補充 3.:客戶留存率與流失率
*補充 4.:Decision Tree 迴歸 Boston
from sklearn.datasets import load_boston
from sklearn.tree import DecisionTreeRegressor as DTR
import pandas as pd
ds = load_boston()
X=pd.DataFrame(ds.data, columns=ds.feature_names)
y=pd.DataFrame(ds.target, columns=['Boston'])
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3)
clf = DTR(max_depth=2, random_state=1)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
>> 0.6865210494380858
.
.
.
.
.
試著用 sklearn 的資料集 breast_cancer,操作 Featuring Extraction (by PCA)。
# Datasets
from sklearn.datasets import load_breast_cancer
import pandas as pd
ds = load_breast_cancer()
df_X = pd.DataFrame(ds.data, columns=ds.feature_names)
df_y = pd.DataFrame(ds.target, columns=['Cancer or Not'])
df_X.head()
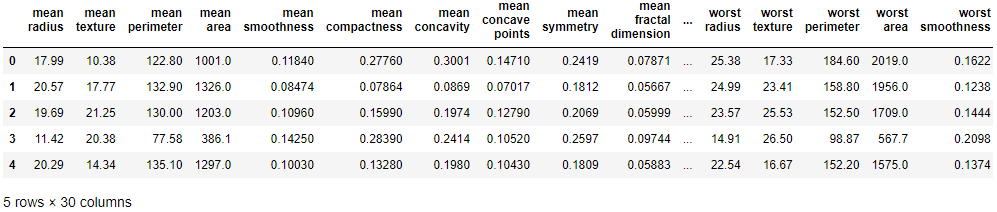
# define y
df_y['Cancer or Not'].unique()
>> array([0, 1])
# Split
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(df_X, df_y, test_size=0.3)
X_train.shape, X_test.shape
>> ((398, 30), (171, 30))
from sklearn.decomposition import PCA
pca1 = PCA(n_components=2)
X_train_pca = pca1.fit_transform(X_train)
X_test_pca = pca1.transform(X_test)
X_train_pca.shape, X_test_pca.shape
>> ((398, 2), (171, 2))
# Modeling (by LogisticRegression)
from sklearn.linear_model import LogisticRegression as lr
clf = lr(solver='liblinear')
clf.fit(X_train_pca, y_train)
print(clf.score(X_test_pca, y_test))
>> 0.9298245614035088
