『電腦科學由於硬體的限制，存在計算的誤差。從同一道數學問題，透過
程式解與手動解析解來觀察此一現象最為顯著。以下將以半徑為1的單位圓內接
正多邊形的周長，反推圓周率 π 來說明。』

圓內接正多邊形的面積、周長公式如下圖：(註)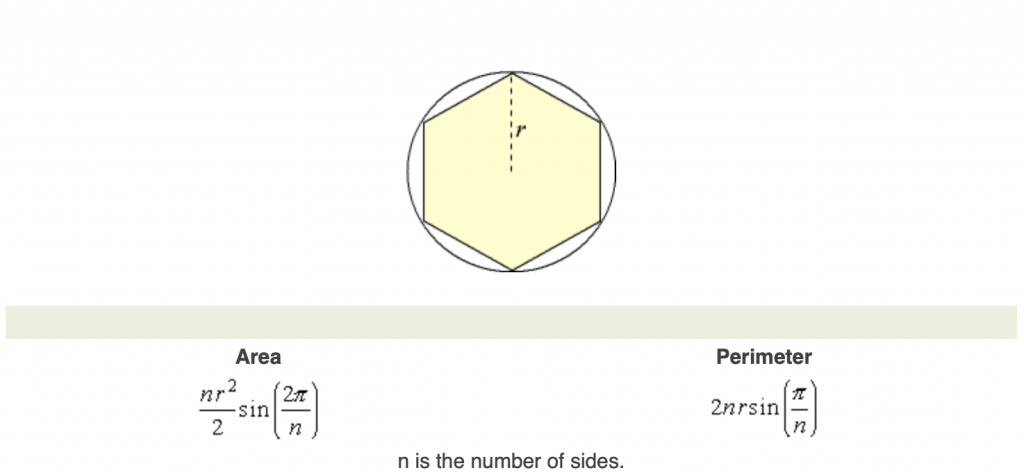

『當 n 無限增大，周長除以 2r 所得到的值，必定隨著 n 增加而增加。 而最終的極限值恰好就是 π。』
可是透過電腦程式的數值解，上述的描述依舊正確嗎？
以下在Repl.it上進行測試。

// π 本身就是超越數，以下限定計算式中用到pi值為-1的反餘弦
double arccos2pi = Math.acos(-1.);

在此就定義在Repl.it執行環境上的正確 π 值為
xxxxxx-circle : 3.141592653589793
以下將觀察正 n 邊形周長除以 2r 後所得到的 π 值與上述 xxxxxx-circle 值進行比較。

double perimeter4radius1circle2pi;
for (int n=最大邊數; n>(最小邊數-1); --n) {
   // 簡化計算式，令 r=1
   perimeter4radius1circle2pi=n*Math.sin(arccos2pi/n);
   
   System.out.println(n+"-circle : " + perimeter4radius1circle2pi);
}

觀察正三角形至正九邊形的結果：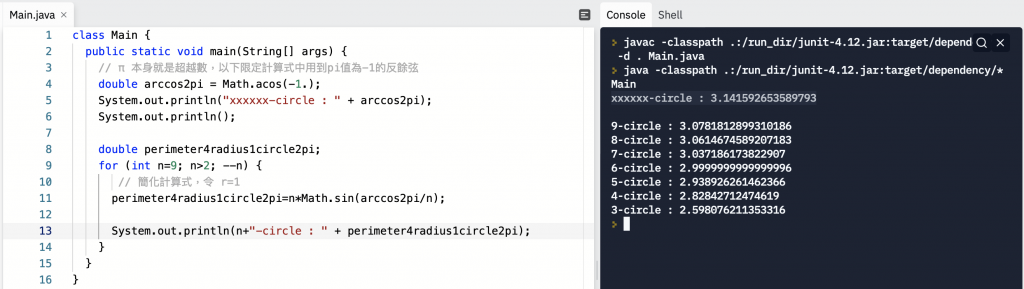

隨著邊數增加，依照多邊形反推計算所得的 π 值越大，越接近 xxxxxx-circle。
目前手算與電腦算都能遵守我們習以為常的數學觀點。
但是，到了 n = 249981 後，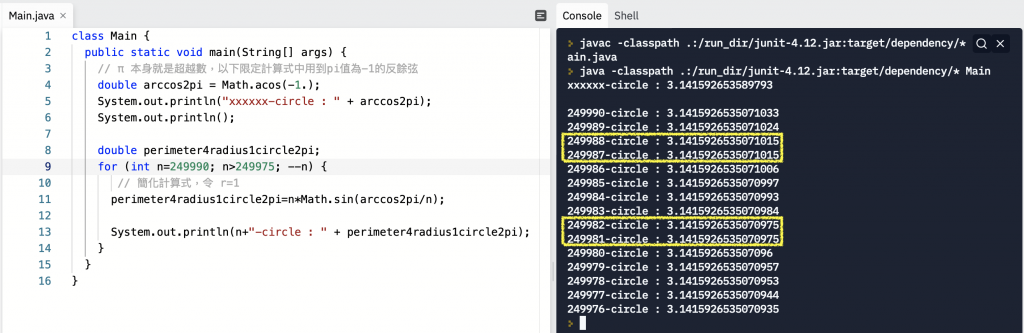

『隨著邊數的增加，所計算出來的 π 值越大的這個規律已經出現問題了。』
甚至到了 n = 999999 時，數值反而又離 xxxxxx-circle 又誤差更大了。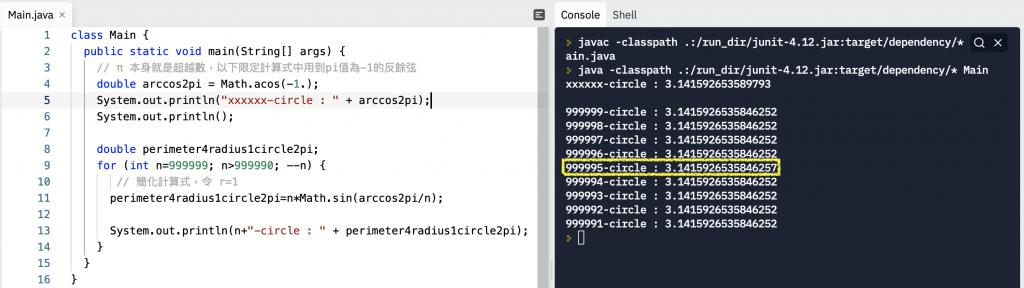

這時候手算因為有效位數能無限延伸，反而沒有此一問題。
『人腦還是比電腦強！』
不過，好消息是，當我們給 n = 2147483647 時，確實就得到 xxxxxx-circle 的值了。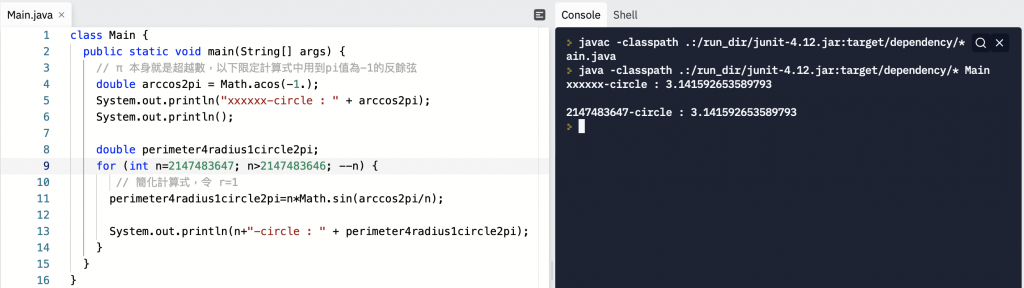

上述案例，當邊數超過某特定值後，所得到的計算值不一定是正確值。直到
給予 int 在電腦上的極限值 2147483647，透過周長反推所計算出的 π
值與 Math.acos(-1) 所得到的值ㄧ致。

2021年，隨著元宇宙(Metaverse)、NFT、...，這類 Web 3.0 的服務相繼崛起。
在分散式的架構下，這類的問題將會越來越顯著。

以 Kubernetes 為例，當所有的分散系統透過 Deployment、Stateful set、Pods
來實現後，在對所有服務設定 『memory request/limit』 的限制下，如
何去測試出在對應的資源中，一些數值的運算極限值，將會大大的影響執行結果及正確性。

真正的困難點在於程式設計師在 Unit Test 的過程中，能否進一步找出
memory request/limit 的合理值，使得在有限的節點上，水平擴展的過程中，所有服
務皆能計算得到可預期的正確結果。
不過『說』還是比較簡單，實際並不容易『做』到。
只能自身技能再提升，

(註)圓內接正多邊形參考網址-https://www.efunda.com/math/areas/PolygonInscribedGen.cfm