今天，IT邦幫忙一直處於當機狀態，天氣之熱，天空卻一滴雨都沒有下，經歷了費波納契數卡關多日的洗禮，我的感受就像被人道殺害的魷魚一樣，痛苦掙扎最後邁向心死的過程。
我想不出來解法，因此參考了他人的程式，然而，展開別人的程式後，我又陷入了因能力不足而痛苦不安的環節，但最後，還是想出了為何這麼做的解釋。

以下是程式:

#include <iostream>
using namespace std;

long long get_pisano_period(long long m)
{
    long long a = 0, b = 1, c = a + b;
    for (int i = 0; i < m * m; i++)
    {
        c = (a + b) % m;
        a = b;
        b = c;
        if (a == 0 && b == 1)
        {
            return i + 1;
        }
    }
}
unsigned long long get_fibonacci_huge_faster(unsigned long long n, unsigned long long m)
{
    n = n % get_pisano_period(m);
    unsigned long long F[n + 1] = {};
    F[0] = 0;
    F[-1] = 1;

    for (int i = 1; i <= n; i++)
    {
        F[i] = F[i - 1] + F[i - 2];
        F[i] = F[i] % m;
    }
    return F[n];
}

int main()
{
    unsigned long long n, m;
    std::cin >> n >> m;
    std::cout << get_fibonacci_huge_faster(n, m) << '\n';
}

Pisano period

沒錯，跟昨日解題的pisano period有關聯，將費波納契數與特定整數相除，該餘數會出現一定的規律，試想一件事，當費波納契數到了一億多值，其實，求他的特定數值餘數，跟不到一千甚至一百左右的費波納契數，並沒有差別。我們只需要抓出以下關鍵數值:

1. 指定整除數的規律數值，例如與3相除，得到8數一循環，規律數值8。
2. 數值整除的餘數值(最終目的)

long long get_pisano_period(long long m)
{
    long long a = 0, b = 1, c = a + b;
    for (int i = 0; i < m * m; i++)
    {
        c = (a + b) % m;
        a = b;
        b = c;
        if (a == 0 && b == 1)
        {
            return i + 1;
        }
    }
}

以上程式是找出餘數規律數，由於可能性位在相除整數平方種可能，因此迴圈數值最後到m^2，只要符合條件就結束迴圈，仔細端詳，該程式與輾轉相除法很類似，但也只是長得像而已。

這是尋找出餘數規律數的程式，我們可以藉此找出規律數。

更新(2022/6/24):

如下圖，假設我們將規律數化為圖型，我們可以一目瞭然，是3一循環，我們選定三角形為初始點(圓形方形也可以)，直到找到下一個三角形時，我們就宣布，找到了循環週期數。然而，數值不會化成形狀，我們要怎麼辨識迴圈已經算到同一情況之指定特徵數值呢?
就是使用程式中的a與b狀態，a, b其實代表著費波納契數值，而求餘數程式，只是將費波納契數限制在有限數值內呈現循環週期態，除了剛開始a=0, b=1，直至下一次a=0, b=1時，我們宣稱找到了週期數，然而，設置的迴圈雖然a, b已經符合return標準，然而迴圈i值來不及更新，因此為彌補這個部分，return i+1。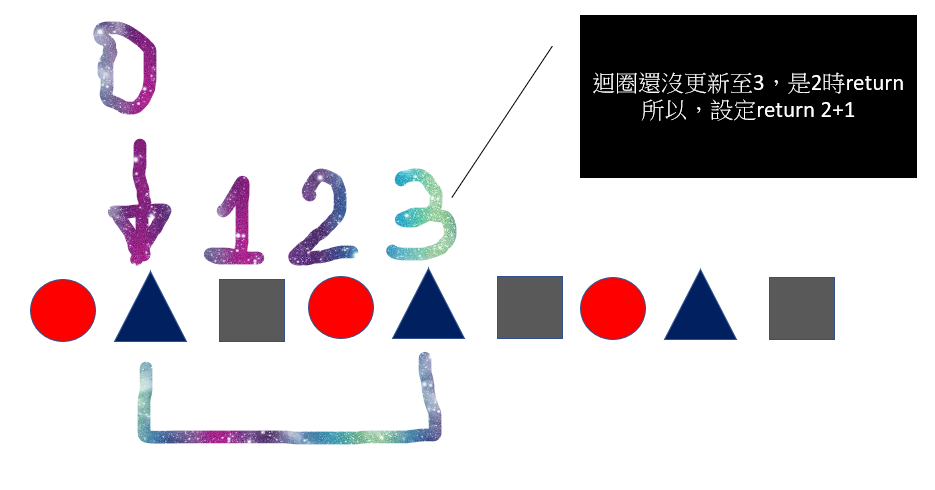

如果我們的整除數是3，那麼該程式會導出8，循環數值。

unsigned long long get_fibonacci_huge_faster(unsigned long long n, unsigned long long m)
{
    n = n % get_pisano_period(m);
    unsigned long long F[n + 1] = {};
    F[0] = 0;
    F[-1] = 1;

    for (int i = 1; i <= n; i++)
    {
        F[i] = F[i - 1] + F[i - 2];
        F[i] = F[i] % m;
    }
    return F[n];
}

以上程式，n為與規律數值相除後的餘數，藉由n製成的迴圈，這樣，我們可以介由較少的計算，最終得到從最小循環數值算起的m之特定餘數，由於只求m的餘數，因此每算一次費波納契數，就留下m的餘數，這會使數值避開overflow又能找出最終餘數的辦法。