I am floating in the most peculiar way.
-- Space Oddity
Note that there is no hard rules on the notations. I will try my best to follow the convention of the hypercubing community.
We already described some basics of the 4D puzzle object back in Day 3, so let's start playing with it today. I will introduce two moves that we will use later in the MC4D software.
Control: Click any non-center cell when pressing Ctrl key.
This move does not actually change the state of the puzzle. A analogy to this move is like rotating a Rubik's Cube as a whole instead of twisting any faces of it. Cubers obeserve the cube with this move before solving. While it looks like we "push" a cell out of our sight, "center" the cell we click, and "summon" a new cell from nowhere, it is just a different 4D perspective to look at this hypercube.
The following video clip demonstrates a sequence, in which I first center the right-front cell (blue), and then the bottom cell (orange), and then the left-front cell (pink).

Don't be confused by the general meaning of rotation. A twist, as a motion, is categorized as a rotation as well. When I want to emphasize the fact that a move is changing the state of the puzzle, I say twist; otherwise, I say rotate or center.
Control: click any sticker.
Let's recall the 3D case first. Twisting a face of a Rubik's Cube is to apply some movement on a part of the puzzle while the other part of the puzzle remains still. The two parts detach each other temporarily, changing the whole shape, and then with enough rotation (90, 180, or 270 degrees) they again reform a cube. The "neighborhood" between the two side of the cut surface before are changed after a twist.
When we are in this good old 3D world, "twist of R face" is mathmatically equivalent to "rotate about X axis". One then may naturally thinks that in 4D world, we rotate a cell about each X/Y/Z/W axises. This statement is correct itself, but I would say it doesn't help us understanding how 4D puzzles work, so it is a misleading way to describe things. Often times, we use intuition to help us understanding some math concepts, but I find it the opposite for hypercubing. Sometimes math provides better clarity for us to seeing into 4D properties.
Strictly speaking, "rotate about X axis" is not a formal way to describe the rotation. Written in the matrix form, as below,
you can almost say it (the top matrix, R_x) has nothing to do with X axis, because no other coordinates contribute to X value after the transformation, and the original X value doesn't contribute to Y and Z coordinates either. Thus, "rotate about X axis" is actually more like "rotate in a manner that Y => Z => -Y => -Z => Y". The later is tedious but applies to all higher dimensions. Saying "rotate about X axis" in 4D space confuses people because "rotate in a manner that Y => Z => -Y => -Z => Y", "rotate in a manner that Y => W => -Y => -W => Y", or other rotation involving multiple axises hold.
Why did I mention "...in 4D world, we rotate a cell about each X/Y/Z/W axises. This statement is correct itself...". For example, the three matrices above can be augmented with a 4th dimension W. The Rx/Ry/Rz rotations can each expand YZ-/XZ-/XY-plane. W axis is perpendicular to these planes, and thus to the basic rotations and even their arbitrary combinations.
The following clip shows how we can twist the center cell, a 3D "slice" of a 4D object, about X (direction from left-back to right-front) and then Y (direction from left-front to right-back) and then Z (direction from bottom to top),
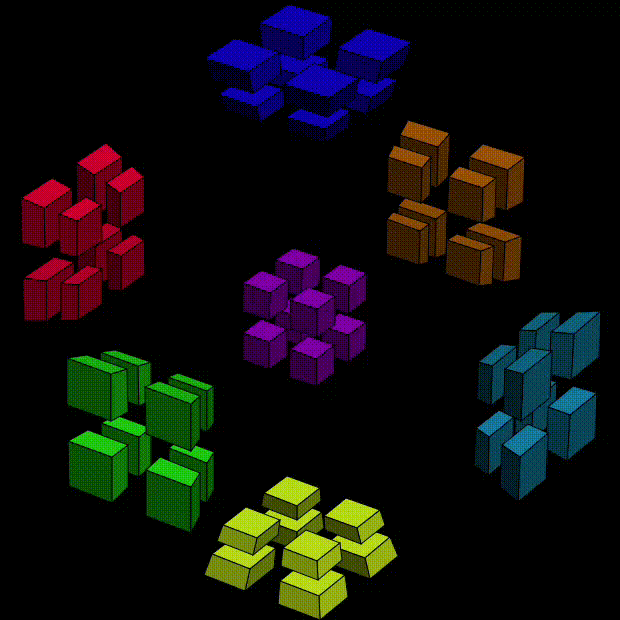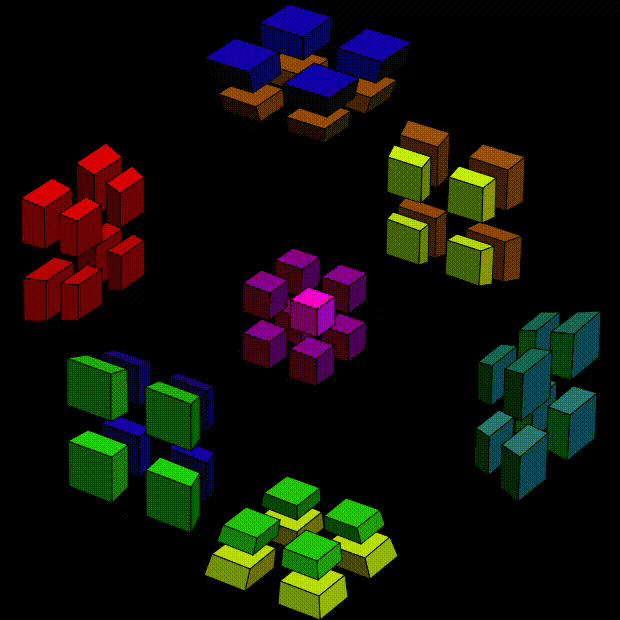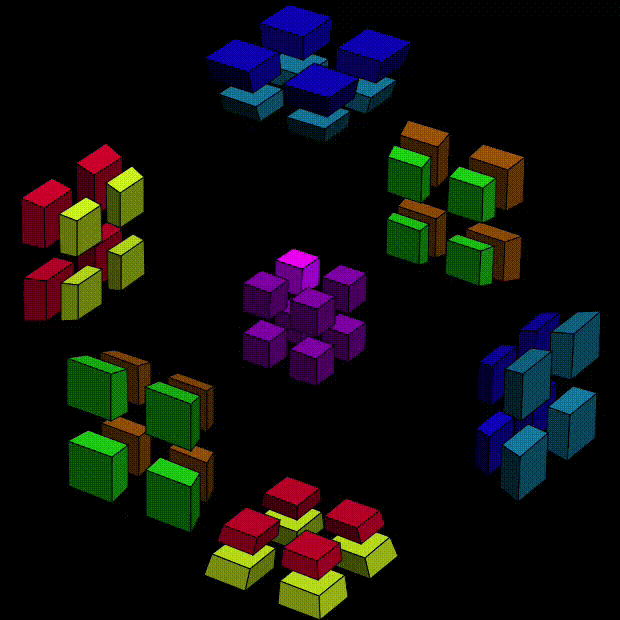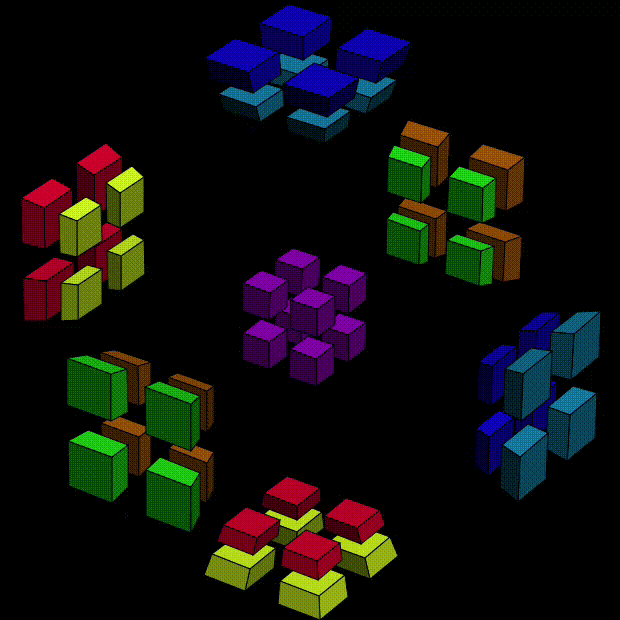
Sorry for that the pointer is not clearly shown. Left/right click (as shown in the clip) results in a counterclockwise/clockwise twist, respectively. The sticker on focus is highlighted. The player must be careful when they clicks the sticker. In the clip, I click on outer faces (facing other cells) instead of internal faces (facing the stickers in the same cell). The former one performs basic twist involving only two dimensions, while the later one performs a more complicated move equivalent to something like X => Y => Z => X. I don't recommand them, at least in the beginning. They can be easily done with two 2-axis basic rotations anyway.
Other than the center cell, one can twist other 6 cells as well. Due to the distorted display, one may have to practice a little bit to fully comprehend the effect of each twist.
MC4D software, its developers, maintainers, and the community that gave birth to it, have my utmost respect. Over decades, the people enjoy extra dimensions and unimaginable puzzles via this piece of software. What have I missed so far? Anyway...
The control of MC4D is introduced. I myself took a few weeks to do the thought experiment, so that the twists is natural to me now. It is not easy at first, but practices won't fail you.
介紹 MC4D 的操作方式。
